Question

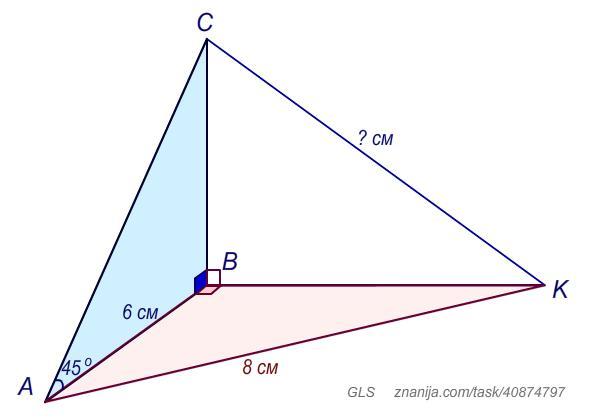
3. Плоскости прямоугольных треугольников АВС и АВК перпендикулярны. АВ=6 см, АК =8 см, АВК=АВС=90°, ВАС =45°. Вычислите расстояние между точками К и С.
Пожалуйста помогите

Answer 1

Ответ:

CK = 8 см.

Объяснение:

1) Рассмотрим прямоугольный ΔABC. По условию ∠BAC = 45°, ∠ABC = 90°, тогда ∠ACB = 45°, т.е. ΔABC равнобедренный.

Тогда BC = AB = 6 см.

2) Прямая AB принадлежит плоскости ΔABC и плоскости ΔABK.

∠ABC = 90°, ∠ABK = 90° по условию.

• Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях (линейный угол двугранного угла).

По условию плоскости треугольников ABC и ABK перпендикулярны.

Тогда угол между плоскостями треугольников - это ∠CBK = 90°. ΔCBK прямоугольный.

3) Треугольники ABK и CBK равны по первому признаку (по двум сторонам и углу между ним):

AB = BC = 6 см, BK - общая сторона, ∠ABK = ∠CBK = 90°.  

Из равенства треугольников следует равенство соответствующих сторон. Гипотенузы этих треугольников равны.

CK = AK = 8 см.