Question

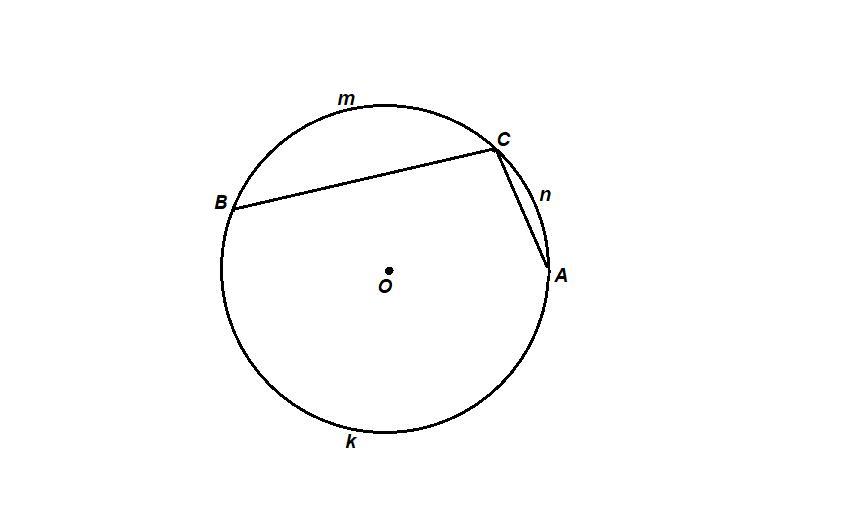
Точки А, В и С лежат на окружности. Вычисли угoл ACB, который образуют хорды AC и BC,
если дуга ∪BmC= 104°, дуга ∪AnC= 47°.

Answer 1

Ответ:

104,5°

Объяснение:

Окружность составляет 360°, поэтому

∪AkB = 360° - (∪BmC + ∪AnC) = 360° - (104° + 47°) = 360° - 151° = 209°

∠АСВ вписанный, опирается на дугу AkB, а вписанный угол равен половине дуги, на которую опирается. Значит,

∠АСВ = 1/2 ∪AkB = 1/2 · 209° = 104,5°