в тетраэдре ABCD, все ребра которого равны 1. Найдите расстояние между AD и BC. Срочно помогите пожалуйста!
Simba2017:
только ответ?
корень из двух пополам.
1/корень из 2
можно решение плиз
Ответы
Ответ дал:
5
Ответ:
Объяснение:
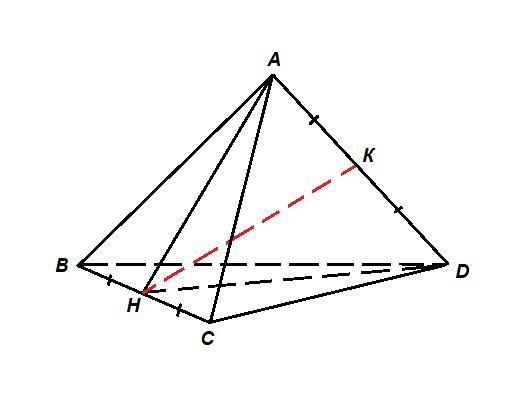
Пусть Н - середина ВС.
Тогда АН⊥ВС и DH⊥ВС как медианы и высоты равносторонних треугольников.
Так как ребро ВС перпендикулярно двум пересекающимся прямым плоскости ADH, то оно перпендикулярно плоскости:
BC⊥(ADH).
Проведем НК - медиану и высоту равнобедренного треугольника АНD (АН = DH = √3/2 как высоты равных равносторонних треугольников).
НК⊂(ADH), BC⊥(ADH), значит ВС⊥НК.
НК⊥AD, значит НК - искомое расстояние между ВС и AD.
ΔАНК: ∠АKH = 90°, АН = √3/2, АК = 1/2, по теореме Пифагора:
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад