Question

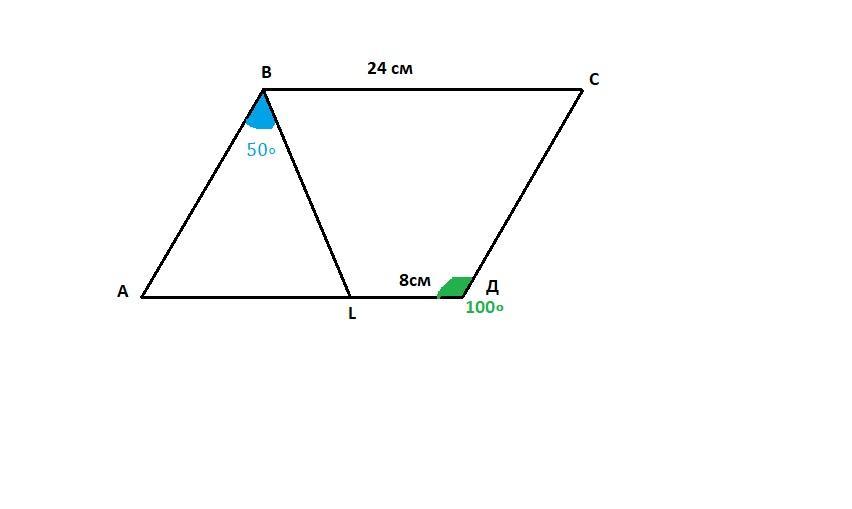
Дан параллелограмм ABCD, ∠D=100∘, BC=24 . На стороне AD есть такая точка L, что ∠ABL=50∘, LD=8. Найдите длину CD.

Answer 1

Ответ:

16 см

Объяснение:

АВСД - параллелограмм

Свойство параллелограмма:

Противоположные стороны параллелограмма равны, противоположные углы параллелограмма равны, а сумма соседних равна 180°.

Следовательно:

• ВС=АД, АВ=СД

•  ∠В=∠Д=100°

∠LBC = ∠B-∠ABL = 100°-50°=50°

∠LBC=∠ALB=50° - как внутренние накрест лежащие углы при параллельных прямых ВС и АД и секущей LB.

⇒ΔABL - равнобедренный ⇒ АВ =АL = АД-LD = 24-8 = 16см

Т.к. АВ=СД, то СД=16см