Question

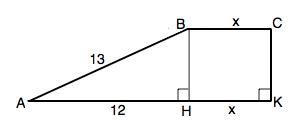
В прямоугольной трапеции АВСК (AKC = 90°) отрезок BH – пер-
пендикуляр, проведенный из вершины В к прямой AK. Найди-
те площадь четырехугольника НВСК, если периметр трапеции
42 см, разность длин ее оснований 12 см, а длина большей боковой стороны 13 см.
вой
13
стороны
см.
32

Answer 1

    В прямоугольной трапеции АВСК (AKC = 90°) отрезок BH – перпендикуляр, проведенный из вершины В к прямой AK. Найдите площадь четырехугольника НВСК, если периметр трапеции 42 см, разность длин её оснований 12 см, а длина большей боковой стороны 13 см.

—————

Ответ: 30 см²

Пошаговое объяснение:  

Четырехугольник НВСК - прямоугольник ( ВС||НК, ВН||СК, ВН и  СК - перпендикуляры).

    Разность длин  оснований трапеции  - отрезок АН=АК-НК=12.

∆ АВН - прямоугольный, с отношением сторон из пифагоровых троек ( 13а:12а:5а), поэтому, поскольку АВ=13 и АН=12, высота трапеции ВН=5.

Р=АВ+ВС+СК+АК=42

Р=13+х+5+х+12=42 =>

2х=42-30=12;

х=6.

Ѕ(НВСК)=ВН•НК=5•6=30 (см²)