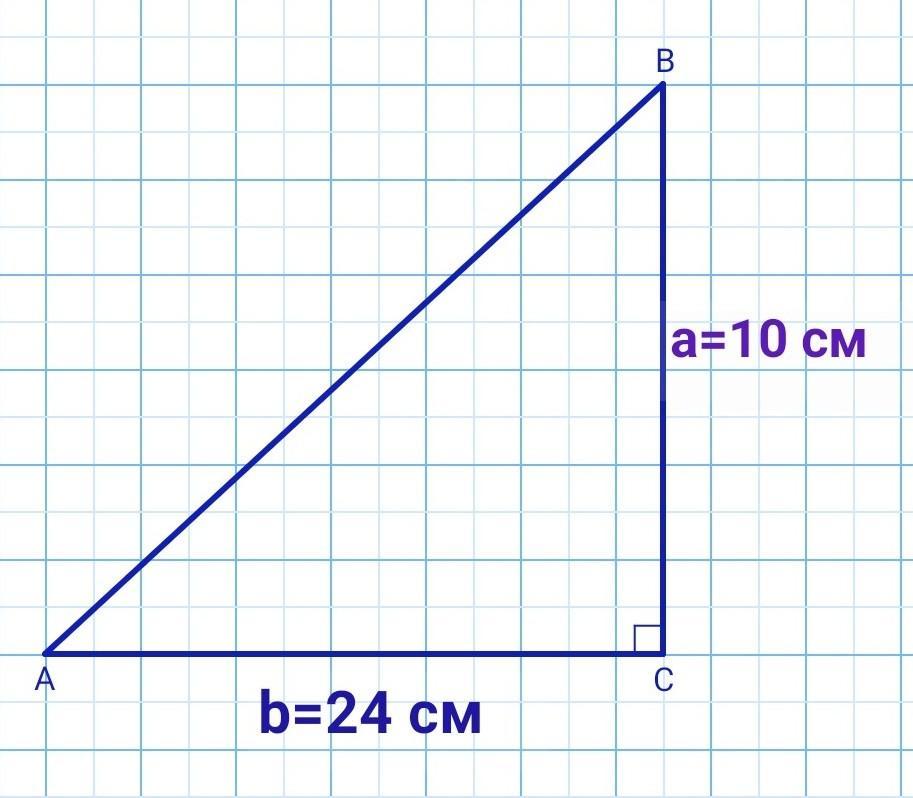
в прямоугольном треугольнике ABC угол c=90° катеты a и b соответственно равны 10 cm и 24 cm найдите гипотенузу c, острые углы Альфа и Бета этого треугольника. Решите задачу двумя способами
ПОЖАЛУЙСТА ВОПРОС ЖИЗНИ И СМЕРТИ!
Ответы
Ответ дал:
24
Ответ:
26 см, 23°, 67°
Объяснение:
1 способ.
По теореме Пифагора найдём гипотенузу АВ:
АВ²=АС²+ВС²=10²+24²=100+576 = 676
АВ=√676=26см
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему: tgA=
Используя таблицу тангенсов. находим, что ∠А≅23°
Так как сумма углов треугольника равна 180°, ∠В = 180-90-23=67°
2 способ.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
Используя таблицу косинусов находим, что ∠В ≅ 67°,
тогда ∠А = 90-67=23°
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад