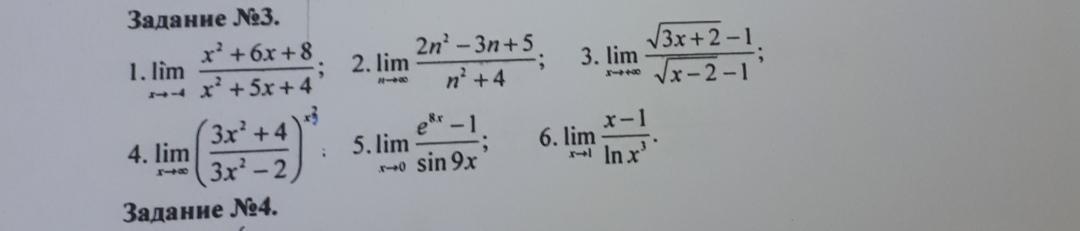Question

Помогите вычислить пределы, пожалуйста

Answer 1

$\displaystyle \sf \boxed{\sf1} \\ \lim_{x \to -4} \frac{x^2+6x+8}{x^2+5x+4}= \lim_{x \to -4} \frac{(x+4)(x+2)}{(x+4)(x+1)}=\lim_{x \to -4} \frac{x+2}{x+1}=\frac{2}{3}$

$\sf \displaystyle \boxed{\sf2} \\ \lim_{n \to \infty} \frac{2n^2-3n+5}{n^2+4}= \lim_{n \to \infty} \frac{n^2\left(2-\dfrac{3}{n}+\dfrac{5}{n^2}\right)}{n^2\left(1+\dfrac{4}{n^2}\right)}= \lim_{n \to \infty} \frac{2-\dfrac{3}{n}+\dfrac{5}{n^2}}{1+\dfrac{4}{n^2}}=2$

$\displaystyle \sf \boxed{\sf3} \\ \lim_{x \to +\infty} \frac{\sqrt{3x+2}-1}{\sqrt{x-2}-1}= \lim_{x \to +\infty} \frac{\sqrt{x}\left(\sqrt{3+\dfrac{2}{x}}-\dfrac{1}{\sqrt{x}}\right)}{\sqrt{x}\left(\sqrt{1-\dfrac{2}{x}}-\dfrac{1}{\sqrt{x}}\right)} =\sqrt{3}$

$\displaystyle \sf \boxed{\sf4} \\ \lim_{x \to \infty} \left(\frac{3x^2+4}{3x^2-2}\right)^{x^2}= \lim_{x \to \infty} \left(1+\frac{6}{3x^2-2}\right)^{x^2}=\lim_{x \to \infty} \left(1+\frac{1}{\dfrac{3x^2-2}{6}}\right)^{x^2\cdot\frac{3x^2-2}{6}\cdot\frac{6}{3x^2-2}}= \\ = \lim_{x \to \infty} exp\left(\frac{6x^2}{3x^2-2}\right)=\lim_{x \to \infty} exp\left(\frac{6}{3-\dfrac{2}{x^2}}\right)=e^2$

$\sf \displaystyle \boxed{\sf5}\\ \lim_{x \to 0} \frac{e^{8x}-1}{sin9x}= \lim_{x \to 0} \frac{8x}{9x}=\frac {8}{9}$

$\displaystyle \sf \boxed{\sf6} \\ \lim_{x \to 1} \frac{x-1}{ln(x^3)}= \lim_{x \to 1} \frac{x-1}{3lnx}= \lim_{t \to 0} \frac{t}{3ln(t+1)}= \lim_{t \to 0} \frac{t}{3t}=\frac{1}{3}$

Пояснения:

4) Применяем второй замечательный предел

lim(1 + (1/x))^x = e  (x → ∞)

5) Пользуемся эквивалентными бесконечно малыми

e^x - 1 = x  (x → 0)

sinx = x  (x → 0)

6) Используем замену переменной и эквивалентность

t = x - 1  ⇒  x = t + 1  ;  (x → 1  ⇒  t → 0)

ln(x + 1) = x  (x → 0)