Срочно очень 30 баллов
Найти производные функций , используя логарифмическую производную.
Приложения:
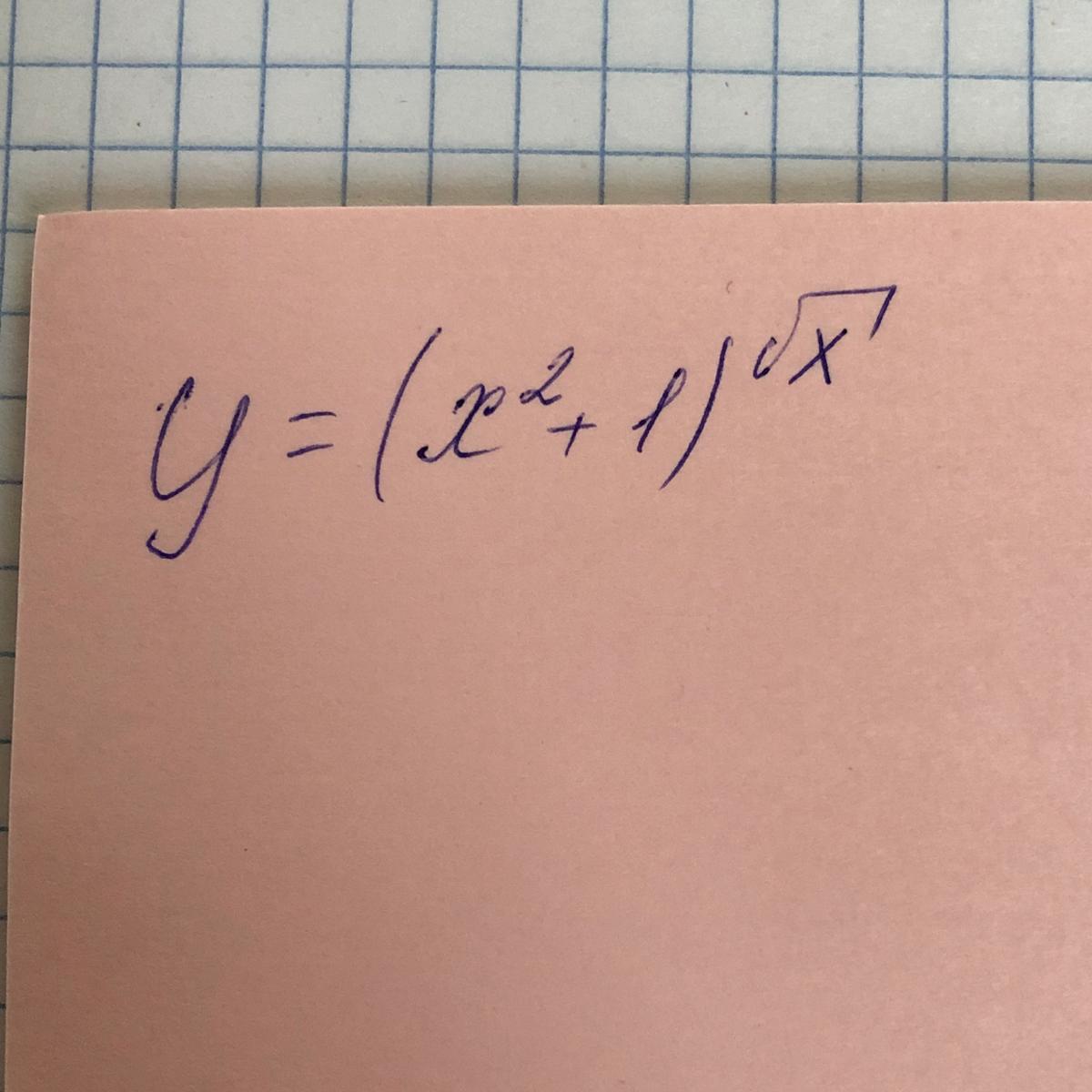
Ответы
Ответ дал:
3
Ответ:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад