Question

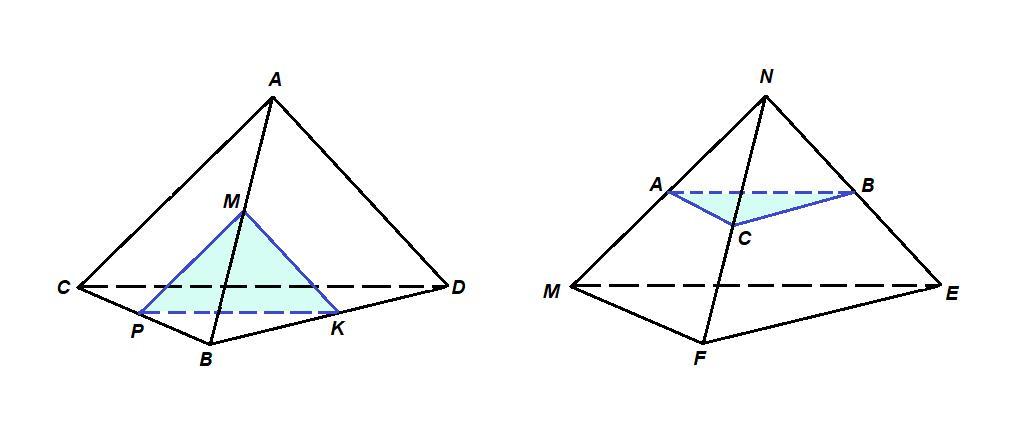
1. В тетраэдре ABCD точки M, K, P – середины рёбер AB, BD и BC.

Докажите, что плоскость MKP параллельна плоскости ACD, и найдите площадь Δ MKP, если площадь Δ ACD равна 96 см².

2. В тетраэдре NMEF точки A, B, C – середины рёбер MN, NE и NF.

Докажите, что плоскость ABC параллельна плоскости MEF, и

найдите площадь Δ MEF, если площадь Δ ABC равна 36 см².

Answer 1

Ответ:

1. 24 см²

2. 144 см²

Объяснение:

МР║АС и МК║AD как средние линии треугольников АВС и ABD соответственно.

• Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.

Значит, (МКР)║(ACD).

МР = 1/2 АС, МК = 1/2 AD, КР = 1/2 CD как средние линии соответствующих треугольников, тогда

ΔМКР ~ ΔADC по трем пропорциональным сторонам.

• Площади подобных треугольников относятся как квадрат коэффициента подобия.

$\dfrac{S_{MKP}}{S_{ADC}}=\dfrac{1}{4}$

$S_{MKP}=\dfrac{S_{ADC}}{4}=\dfrac{96}{4}=24$ см²

2. АВ║МЕ и АС║MF как средние линии треугольников NME и NMF соответственно.

• Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.

Значит, (ABC)║(MEF).

AB = 1/2 ME, BC = 1/2 EF,  AC = 1/2 MF

как средние линии соответствующих треугольников, тогда

ΔАВС ~ ΔMEF по трем пропорциональным сторонам.

• Площади подобных треугольников относятся как квадрат коэффициента подобия.

$\dfrac{S_{ABC}}{S_{MEF}}=\dfrac{1}{4}$

$S_{MEF}=S_{ABC}\cdot 4=36\cdot 4=144$  см²