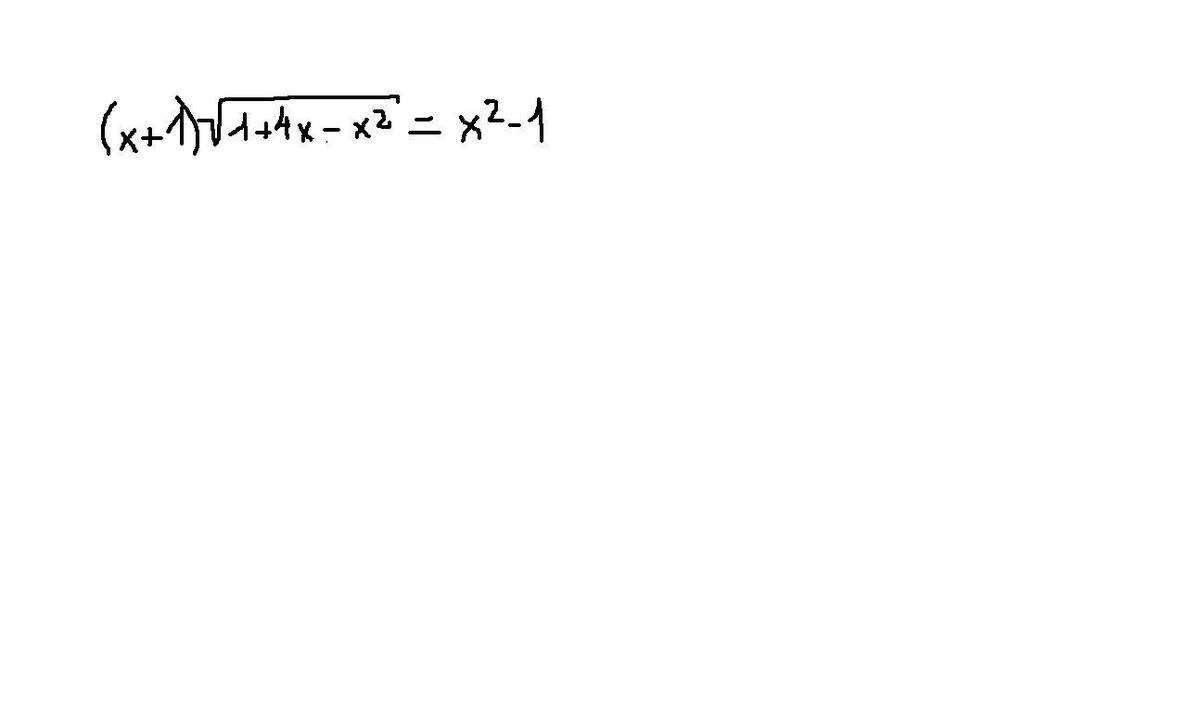Ответы
Ответ дал:
0
Условие:(x+1)√1+4x-x²=x²-1
Решение: запишем ОДЗ. под корнем должно быть ≥0. ⇒x²-4x-1≤0
x∈[2-√5;2+√5] - из первого. x²-1≥0... тут x∈(- беск. до -1. и от 1 до +беск)... Общее ОДЗ будет х[1; 2+√5]
Решение: (x+1)√1+4x-x²=(x-1)(x+1)
√1+4x-x²=x-1
1+4x-x²=x²-2x+1
-2x²+6x=0
2x(-x+3)=0
x1=0 ; x2=3.....смотрим на одз... x=0 - не подходит... х=3 - удовлетворяет . Ответ: x=3
Решение: запишем ОДЗ. под корнем должно быть ≥0. ⇒x²-4x-1≤0
x∈[2-√5;2+√5] - из первого. x²-1≥0... тут x∈(- беск. до -1. и от 1 до +беск)... Общее ОДЗ будет х[1; 2+√5]
Решение: (x+1)√1+4x-x²=(x-1)(x+1)
√1+4x-x²=x-1
1+4x-x²=x²-2x+1
-2x²+6x=0
2x(-x+3)=0
x1=0 ; x2=3.....смотрим на одз... x=0 - не подходит... х=3 - удовлетворяет . Ответ: x=3
Ответ дал:
0
вы молодцы, благодарю за решение...
Ответ дал:
0
Почему x не может быть равен 0?
Ответ дал:
0
По ОДЗ... в таких уравнениях можно сделать проверку , тем самым показать, какой корень подходит а, а какой нет.
Ответ дал:
0
спасибо!
Вас заинтересует
2 года назад
8 лет назад
10 лет назад
10 лет назад
11 лет назад