Question

в прямоугольном треугольнике ABC угол C равен 90 градусов гипотенуза равна 25 см катет равен 24 см найдите катет и острый угол Альфа и Бета Решите задачу двумя способами​

Answer 1

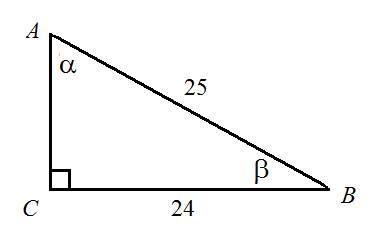
См. рисунок.

Пусть дан ΔАВС, ∠С = 90°, АВ = 25 см, ВС = 24 см, ∠А = α, ∠В = β.

Найдем АС, α и β.

1-й способ.

По теореме Пифагора АС² = АВ² - ВС² = 25² - 24² = 625 - 576 = 49, откуда АС = 7 (cм).

sinα = ВС : АВ = 24 : 25 = 0,96, откуда ∠α = arcsin0,96 ≈ 74°.

∠β = ∠В = 90° - ∠A = 90° - ∠α ≈ 90° - 74° = 16°.

2-й способ.

соsβ = ВС : АВ = 24 : 25 = 0,96, откуда ∠β = arcсоs0,96 ≈ 16°.

sinα = ВС : АВ = 24 : 25 = 0,96, откуда ∠α = arcsin0,96 ≈ 74°.

Т.к. sin²α + соs²α = 1 и α - острый угол, то

cos²α = 1 - sin²α = 1 - 0,9216 = 0,0784, откуда соsα = √0,0784 = 0,28, следовательно, АС = АВ · соsα = 25 · 0,28 = 7 (см).

Ответ: 7 см, 74° и 16°.