Question

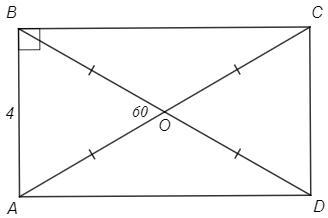
Угол между диагоналями прямоугольника равен 60°.
Найдите площадь прямоугольника, если меньшая его сторона равна 4.
Ответ: 16 корней из 3
Нужно решение

Answer 1

Диагонали прямоугольника равны и точкой пересечения делятся пополам.

OA=OB=OC=OD

△AOB - равнобедренный с углом 60 - равносторонний, OA=AB

AB=x, AC=2x

BC =√(AC^2 -AB^2) =x√(4-1) =x√3 (т Пифагора)

AB=4, BC=4√3

S(ABCD) =AB*BC =4 *4√3 =16√3