Прямоугольник имеет стороны 2 см и 8 см.
а) Найдите площадь квадрата, периметр которого равен периметру данного прямоугольника.
Ответы
Ответ дал:
1
))))))))))))))))))))))))))))))
Приложения:
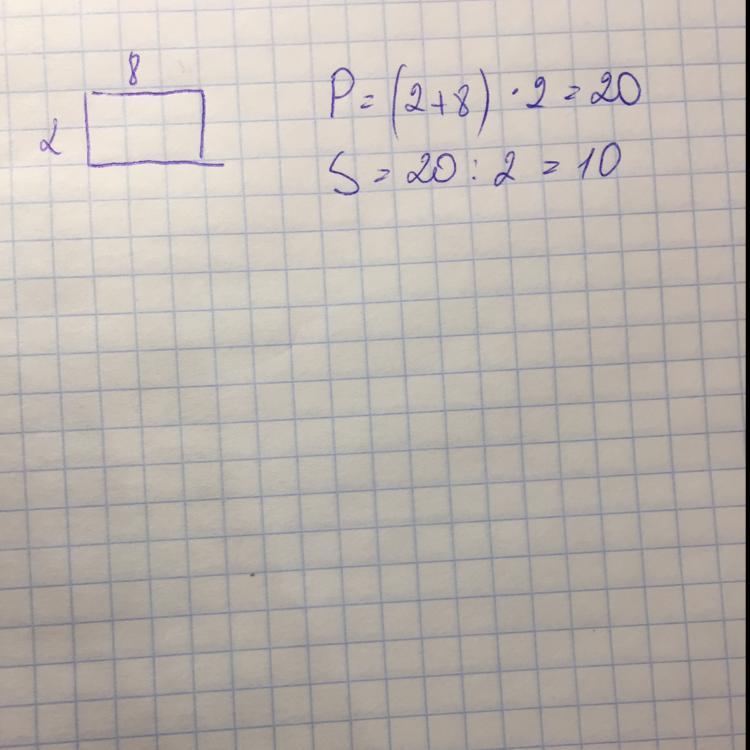
arinazaharova2006:
Я тут не доделала действие, получается одна сторона 5 и площадь 5*5=25
спасибо
То есть надо было: (8+2)*2=20
20:4=5 и 5*5=25 вот так)))
20:4=5 и 5*5=25 вот так)))
Извиняете пожалуйста
Если не понятно могу объяснить
ничего
нет вроде понятно
Хорошо, а какой это класс?
вв..в 55555
Ответ дал:
1
Ответ:
Площадь квадрата равен 25 см кв;
Решение:
Площадь квадрата находится по формуле: а*а
т.к. у квадрата все стороны равны;
Чтобы найти площадь квадрата, для начала нужно узнать его периметр.
Нам известно, что периметр квадрата равен периметру прямоугольника.
Формула нахождения периметра прямоугольника: (а+b)*2
Подставляем и получаем: (2+8)*2 = 10*2 = 20 (см);
P(прямоугольника) = 20 (см)
По условию сказано, что периметр прямоугольника равен периметру квадрата значит:
P(квадрата) = 20 (см)
Осталось узнать, чему равны стороны квадрата, для вычисления его площади.
Известно, что все стороны у квадрата равны, соответственно вспомним формулу нахождения периметра квадрата:
P(квадрата) = 4*а (т.к. у квадрата 4 стороны), значит составим уравнение:
20 = 4*а
Вспомним, для того, чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
а = 20:4
а = 5 (см)
Ответ: сторона квадрата равна 5 см.
Всё известное у нас имеется, соответственно, находим площадь:
S(квадрата) = 5*5 = 25 (см кв.)
Ответ: площадь квадрата равна 25 см кв.
Площадь квадрата равен 25 см кв;
Решение:
Площадь квадрата находится по формуле: а*а
т.к. у квадрата все стороны равны;
Чтобы найти площадь квадрата, для начала нужно узнать его периметр.
Нам известно, что периметр квадрата равен периметру прямоугольника.
Формула нахождения периметра прямоугольника: (а+b)*2
Подставляем и получаем: (2+8)*2 = 10*2 = 20 (см);
P(прямоугольника) = 20 (см)
По условию сказано, что периметр прямоугольника равен периметру квадрата значит:
P(квадрата) = 20 (см)
Осталось узнать, чему равны стороны квадрата, для вычисления его площади.
Известно, что все стороны у квадрата равны, соответственно вспомним формулу нахождения периметра квадрата:
P(квадрата) = 4*а (т.к. у квадрата 4 стороны), значит составим уравнение:
20 = 4*а
Вспомним, для того, чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
а = 20:4
а = 5 (см)
Ответ: сторона квадрата равна 5 см.
Всё известное у нас имеется, соответственно, находим площадь:
S(квадрата) = 5*5 = 25 (см кв.)
Ответ: площадь квадрата равна 25 см кв.
спасибо
Вас заинтересует
2 года назад
2 года назад
8 лет назад