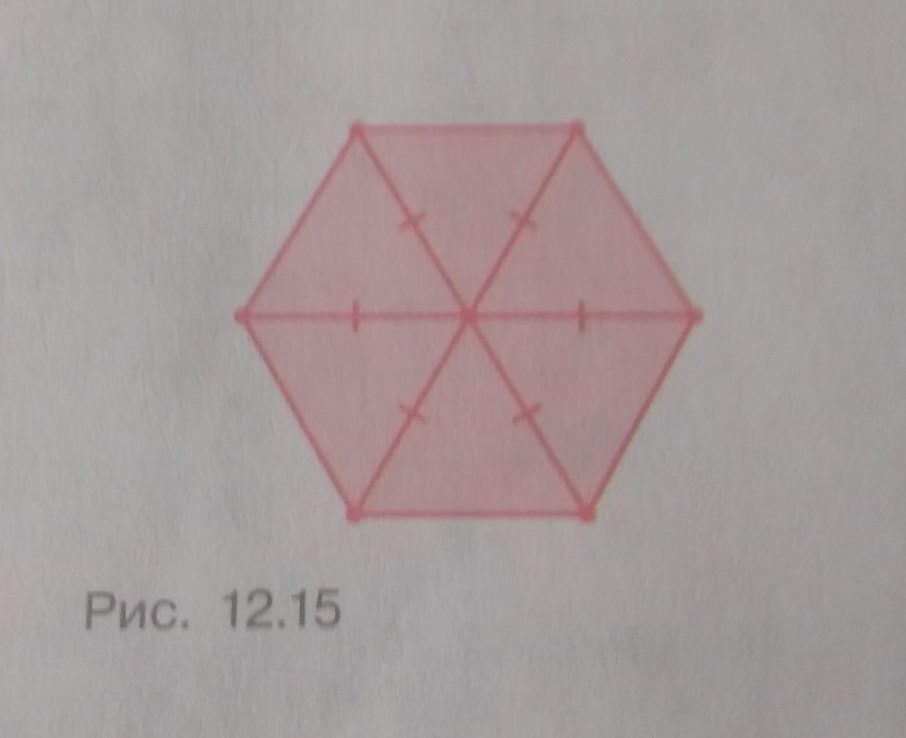
все стороны выпуклого шестиугольника равны. Внутри него оказалась точка, которая находится на одинаковых расстояниях от всех его вершин. Докажите, что все углы этого шестиугольника тоже равны
Приложения:
MakBata2007:
чесно говоря самому нужен ответ)))
Ща, я уже не помню прорешали мы его все таки или нет. если да, то скину, бро
Ответы
Ответ дал:
26
Ответ:
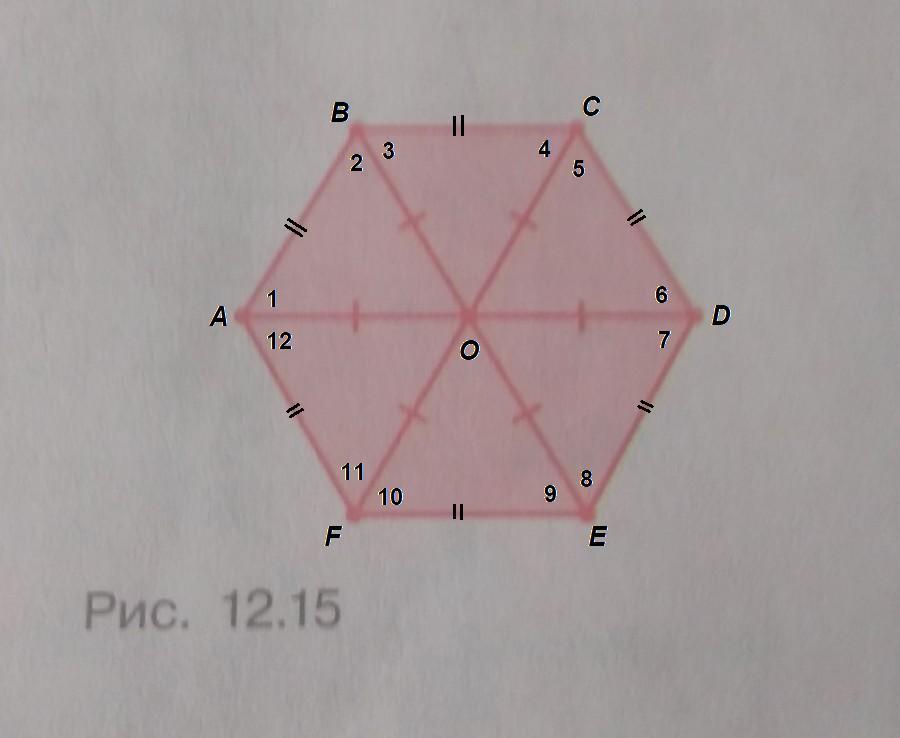
Пусть О - точка, равноудаленная от всех вершин шестиугольника, т.е
ОА = ОВ = OC = OD = OE = OF
ΔАОВ равнобедренный, ∠1 = ∠2.
Все шесть треугольников равны по трем сторонам, значит равны все углы при основаниях этих треугольников:
∠1 = ∠2 = ... = ∠12
У шестиугольника:
∠А = ∠12 + ∠1, ∠В = ∠2 + ∠3 и так далее.
Значит, ∠А = ∠B = ∠C = ∠D = ∠E = ∠F.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад