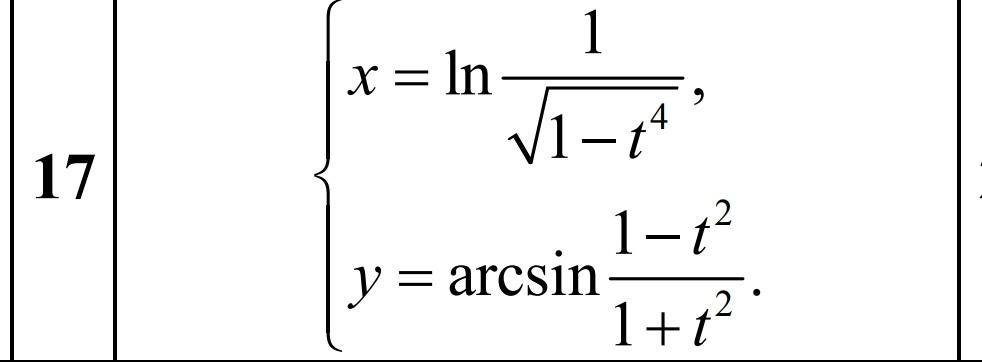
Ответы
Ответ дал:
1
Ответ:
stsofya:
большое спасибо
внимательно проверьте все сокращения за мной и тд)
не исключаю ошибку
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад