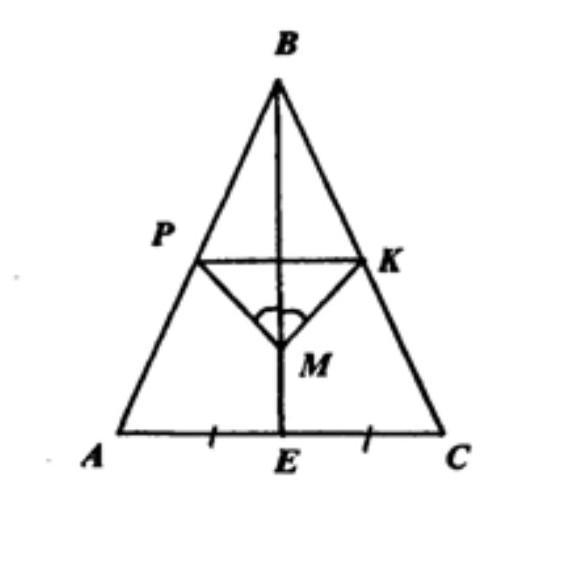
В треугольнике АВС АВ=ВЕ. На медиане ВЕ отмечена точка М, а на сторонах АВ и ВС - точки Р и К соответственно (точки Р М К не лежат на одной прямой). Известно, что угол ВМР равен углу ВМК. Докажите, что углы ВРК и ВКМ равны
очень прошу, сначала пишите в комментарии, а потом уже в ответы!
siestarjoki:
условие неверно записано
https://znanija.com/task/1011006
ок
поняла
но там странное решение.
Равнобедренный треугольник, медиана является биссектрисой. Треугольники BPM и BKM равны по стороне (общая) и прилежащим углам.
да
признаю что решение правильное
но мне ещё к этому решению надо найти чертёж...
Ответы
Ответ дал:
0
Объяснение:
AB=BC, следовательно ∆АВС — равнобедренный. Значит ВМ— биссектриса
∠PBM = ∠MBK ⇒ ∠BPM= ∠BKM
Приложения:
Кстати, нельзя сначала писать в комменты , а потом в ответы , так как комменты появляются как бы после ответа . Это так, на будущее )
я знаю
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад