Ответы
Ответ:
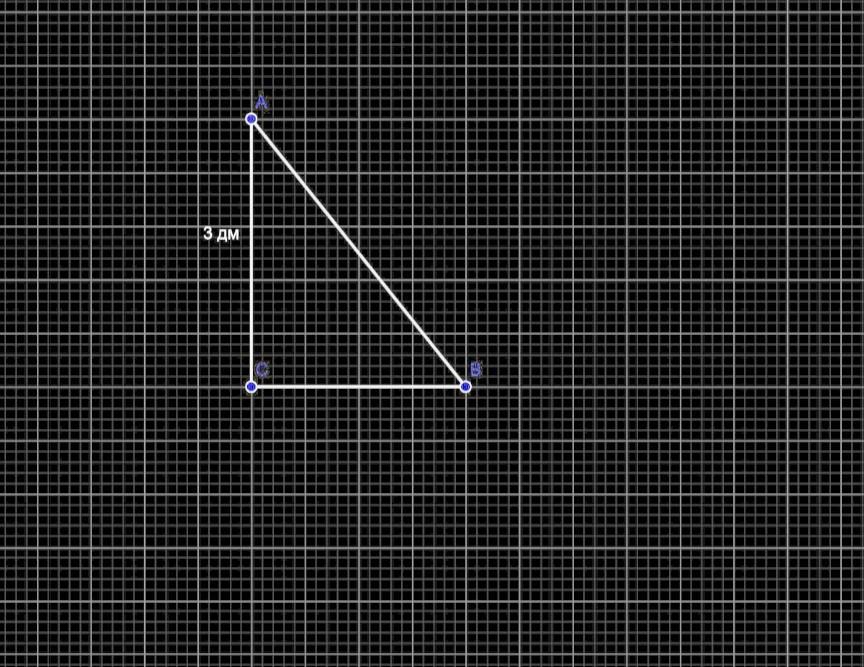
AB= 3,4 дм, BC= 1,6 дм.
Объяснение:
Воспользуемся основным тригонометрическим тождеством
sin^{2} x+cos^{2} x=1.sin
2
x+cos
2
x=1.
Найдем синус угла B
\begin{gathered}sin^{2}B=1- cos^{2} B;\\sinB =\pm \sqrt{1-cos^{2}B } ;\end{gathered}
sin
2
B=1−cos
2
B;
sinB=±
1−cos
2
B
;
В прямоугольном треугольнике
\begin{gathered}sinB= \sqrt{1-cos^{2}B } ;\\ sinB=\sqrt{1- (\frac{8}{17})^{2} } =\sqrt{1-\frac{64}{289} } =\sqrt{\frac{289}{289 } -\frac{64}{289} } = \sqrt{\frac{225}{289} } = \frac{15}{17}\end{gathered}
sinB=
1−cos
2
B
;
sinB=
1−(
17
8
)
2
=
1−
289
64
=
289
289
−
289
64
=
289
225
=
17
15
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе
\begin{gathered}sinB=\frac{AC}{AB} ;\\\\\frac{15}{17} =\frac{3}{AB} ;\\\\AB= \frac{17*3}{15} = \frac{17}{5} =\frac{34}{10} =3,4\end{gathered}
sinB=
AB
AC
;
17
15
=
AB
3
;
AB=
15
17∗3
=
5
17
=
10
34
=3,4
AB= 3,4 дм.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе
\begin{gathered}cos B= \frac{BC}{AB} ;\\\\BC= AB* cosB;\\BC= \frac{17}{5} * \frac{8}{17} =\frac{8}{5} =\frac{16}{10} =1,6\end{gathered}
cosB=
AB
BC
;
BC=AB∗cosB;
BC=
5
17
∗
17
8
=
5
8
=
10
16
=1,6
BC= 1,6 дм.