Ответы
Ответ дал:
1
Ответ:
-2; 2 эти корни
Объяснение:
всё на фото
Приложения:
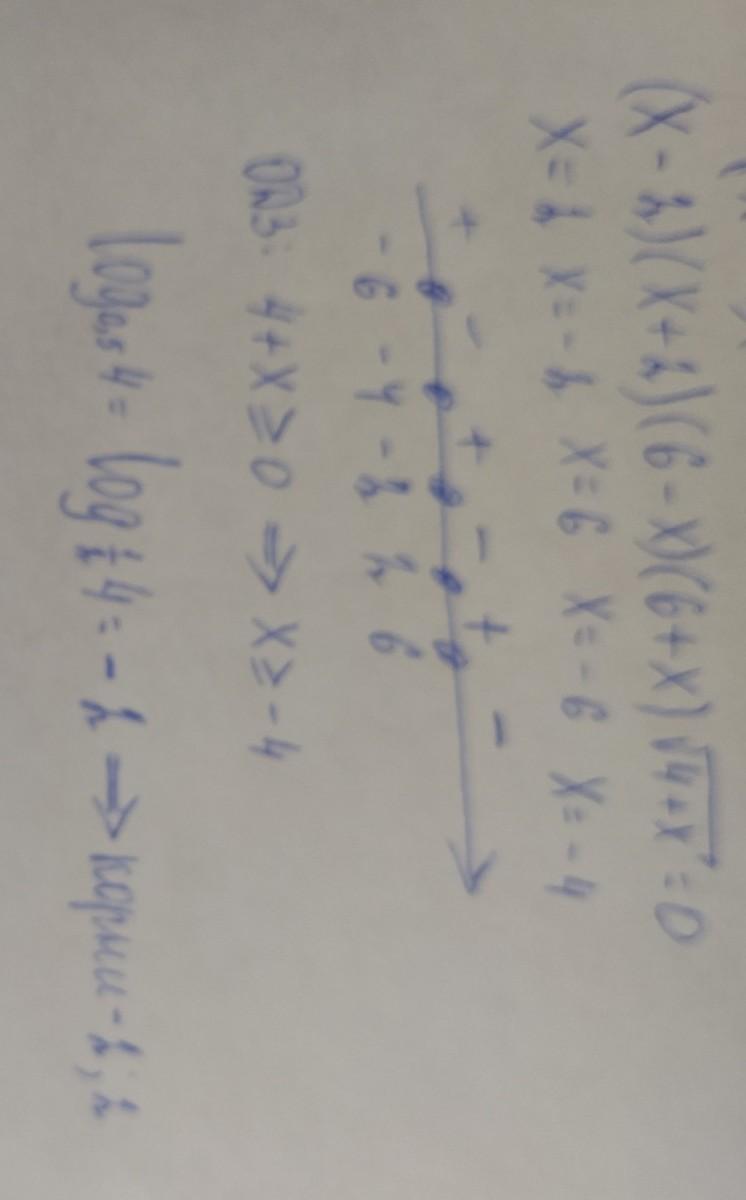
abdullaevislam935:
Это и есть ответ?
Ответ дал:
1
Ответ:
Объяснение:
ОДЗ:
Решение:
Корень –6 не удовлетворяет ОДЗ.
Рассмотрим приведённый отрезок:
В приведённый отрезок не входят корни –4 и 6.
Итоговый ответ:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
