Очень срочно,
ЗАПИШИТЕ 4 ПЕРВЫХ ЧЛЕНА БЕСКОНЕЧНО УБЫВАЮЩЕЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ (bn(n-маленькая) и найдите ее сумму.Нужно полное решение,а не только ответ
Приложения:
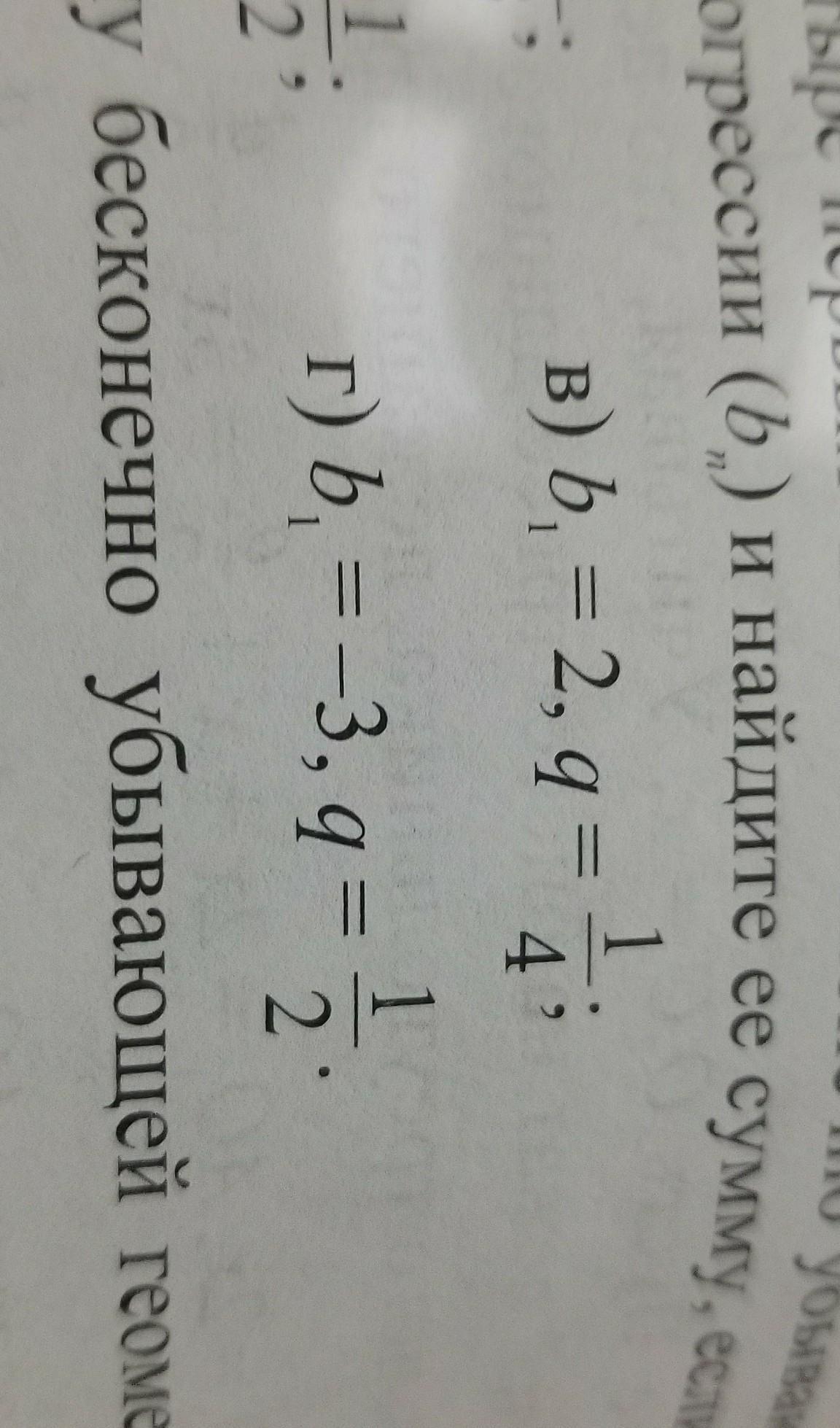
Ответы
Ответ дал:
21
в)
г)
sukhoparova05:
Огромное спасибо
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад