Question

1.Площадь квадрата равна 49см^2.Найдите периметр этог квадата
2.Перимет-р прямоугольника равен 17 см, одна из его сторон на 3 см больше другой.Найдите площадь этого прямоугольника
3.Периметр прямоугольника равен 26 см, а одна из его смежных сторон равна 9см.Прямоугольник имеет такую же площадь, что и квадрат. Найдите периметр квадрата

Answer 1

Ответ:

решение на фото

Пошаговое объяснение:

................

Answer 2

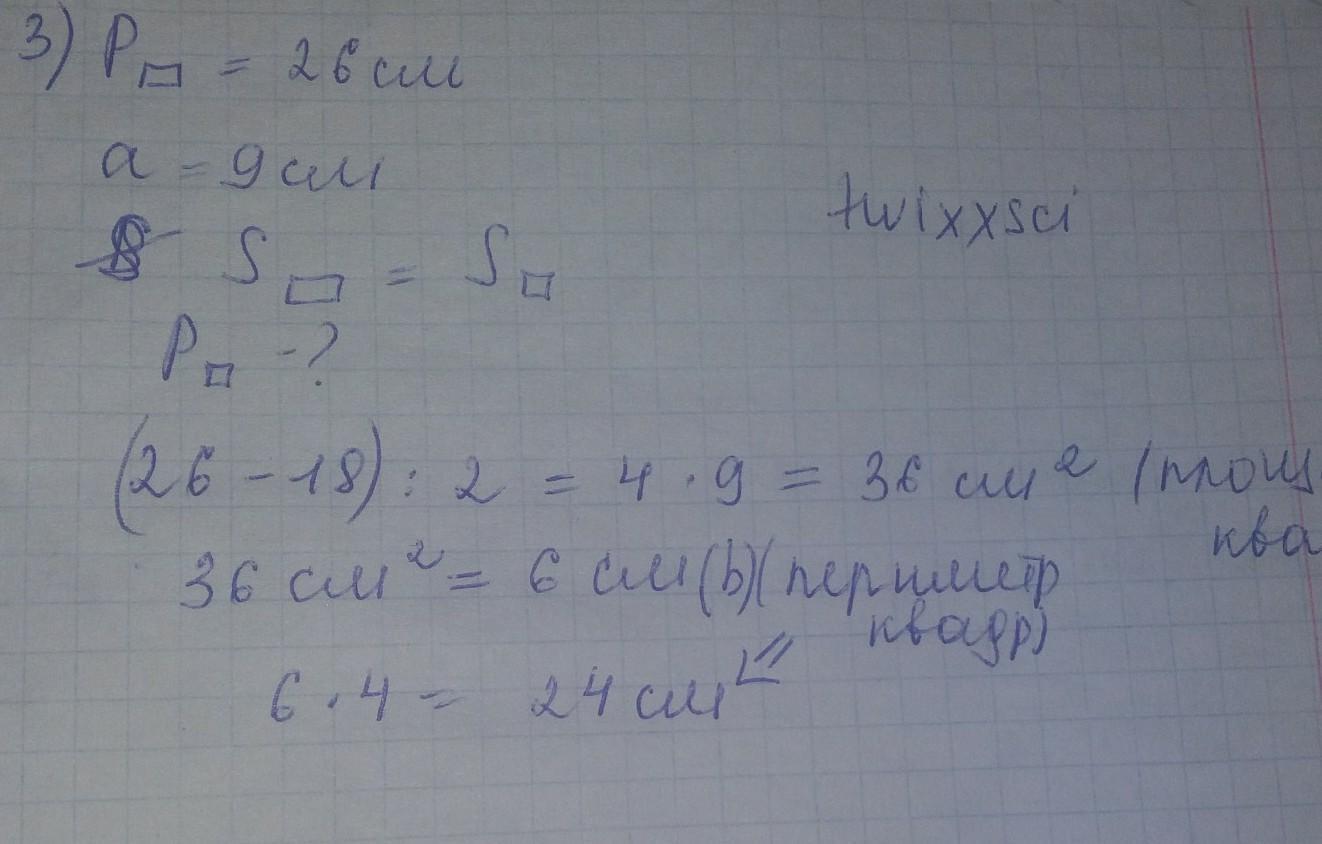
1. Площадь квадрата равна длине его стороны, возведённой в квадрат:  $S = a^2$, где $a$ - это сторона квадрата. Зная площадь, можем вычислить длину стороны: $a = \sqrt{S} = \sqrt{49} = 7$ см. Периметр квадрата равен длине его стороны, умноженной на 4:  $P = 4a = 4\cdot 7 = \boxed{\textbf{28}}$ см.

2. Периметр прямоугольника равен удвоенной сумме его смежных сторон. Пусть $a$ см - одна из сторон прямоугольника, а другая сторона на 3 см больше, то есть, $(a+3)$ см. Составляем уравнение:

$2(a+a+3) = 17\\\\2(2a+3) = 17\\\\4a + 6 = 17\\\\4a = 11\\\\a = \boxed{2,75}$

Тогда другая сторона его  $2,75 + 3 = \boxed{5,75}$ см.

Площадь прямоугольника равна произведению длин его смежных сторон, тогда  $S = 2,75 \cdot 5,75 = \boxed{\textbf{15,8125}}$ см².

3. Для начала найдём вторую сторону прямоугольника. Периметр прямоугольника равен удвоенной сумме его смежных сторон, тогда:

$2(9+x) = 26\\\\18 + 2x = 26\\\\2x = 8\\\\x = \boxed{4}$

Тогда площадь прямоугольника  $S = 9\cdot 4 = \boxed{36}$ см².

Прямоугольник имеет такую же площадь, что и квадрат. Площадь квадрата равна длине его стороны, возведённой в квадрат:  $S = a^2$, где $a$ - это сторона квадрата. Зная площадь, можем вычислить длину стороны: $a = \sqrt{S} = \sqrt{36} = 6$ см. Периметр квадрата равен длине его стороны, умноженной на 4:  $P = 4a = 4\cdot 6 = \boxed{\textbf{24}}$ см.