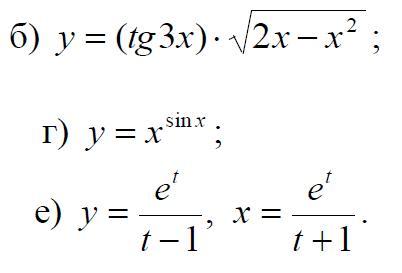Ответы
Ответ дал:
2
Ответ:
б)
г)
По формуле:
е)
По формуле:
Ифигения:
Огромное спасибо!
завтра еще ДУ порешаю)
<3
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад