Question

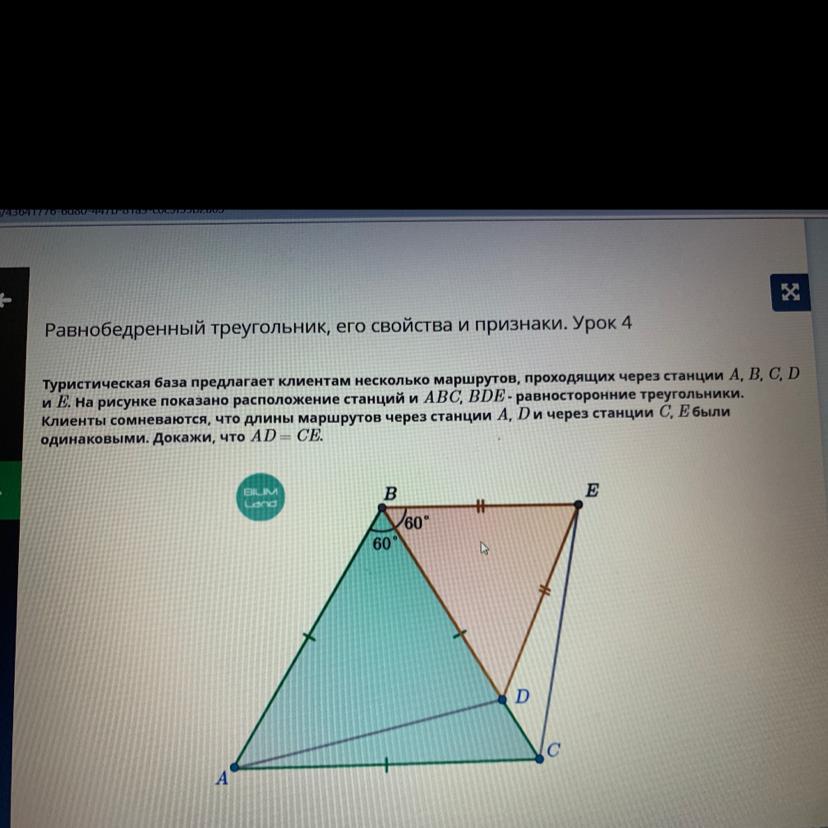
Туристическая база предлагает клиентам несколько маршрутов, проходящих через станции А, В, С, D
и E. На рисунке показано расположение станций и ABC, BDE - равносторонние треугольники.
Клиенты сомневаются, что длины маршрутов через станции А, D и через станции С, Е были
одинаковыми. Докажи, что AD = СЕ.

Answer 1

Ответ:

Во-первых, так как треугольник ABC – равносторонний,

то ∠ABD = 60°.

Во-вторых, так как треугольник BDE – равносторонний,

то ∠DBE = 60°.

Тогда в треугольниках ABD и CBE:

AB = BC, BD = BE, ∠ABD = ∠DBE = 60°.

По первому признаку равенства треугольников

ΔABD = ΔCBE.

Следовательно, AD = CE

Объяснение: