Question

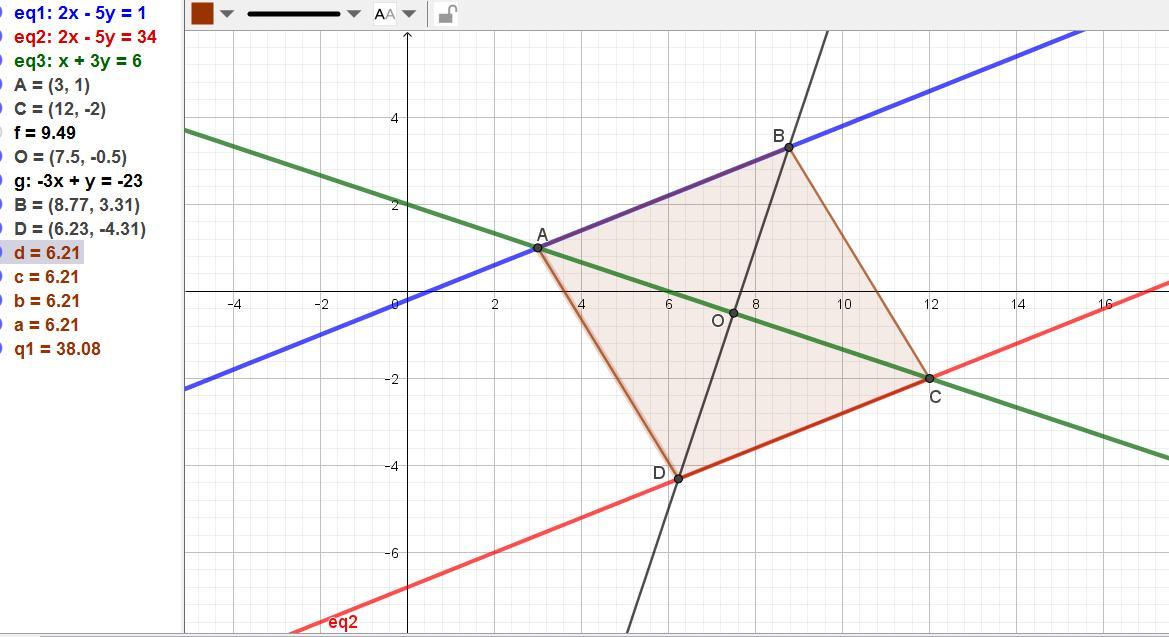
Даны уравнения двух сторон ромба 2x-5y-1=0, 2x-5y-34=0 и уравнение одной диагонали x+3y-6=0. составить уравнение второй диагонали ромба

Answer 1

Пошаговое объяснение:

на словах:

находите точки пересечения диагонали с двумя сторонами решая системы уравнений

2х-5у-1=0

х+3у-6=0

и вторая система

2х-5у-34=0

х+3у-6=0

найдя координаты точек пересечения, находите середину отрезка диагонали

и проводите к ней прямую перпендикулярную к первой диагонали

в аналитической геометрии перпендикулярность это произведение угловых коэффициентов прямых равно 1

Answer 2

Даны уравнения двух сторон ромба 2x-5y-1=0, 2x-5y-34=0 и уравнение одной диагонали x+3y-6=0.

Находим 2 вершины ромба как точки пересечения сторон с диагональю.

{2x-5y-1=0,              2x-5y-1=0

{x+3y-6=0  |x(-2) = -2x-6y+12=0

                                  -11y +11 = 0, отсюда у = 11/11 = 1,

тогда х = 6 - 3у = 6 -3*1 = 3. Точка А(3; 1).

{2x-5y-34=0,              2x-5y-34=0

{x+3y-6=0  |x(-2) =   -2x-6y+12=0

                                  -11y - 22 = 0, отсюда у = -22/11 = -2,

тогда х = 6 - 3у = 6 -3*(-2) = 12. Точка С(12; -2).

Находим координаты точки О как середины отрезка АС.

О = ( А(3; 1) + С(12; -2))/2 = (7,5; -0,5).

Вектор АС =  (С(12; -2) -  ( А(3; 1)) = (9; -3).

Уравнение АС: дано в задании: x+3y-6=0.

В уравнении перпендикуляра к АС коэффициенты А и В меняются на -В и А: -3x + y + С = 0 Подставим координаты точки О.

-3*7,5 + (-0,5) + С = 0, отсюда С = 23.

Ответ: уравнение ВD: -3x + y + 23 = 0 или с положительным коэффициентом при переменной "х": 3х - у - 23 = 0.