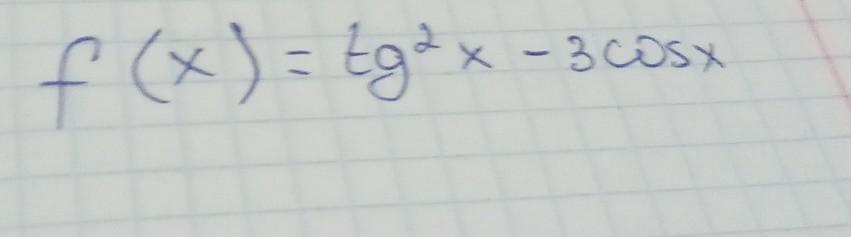Question

помогите найти производную​

Answer 1

Ответ:

2sin(x)/cos(x)^3 + 3sinx

Объяснение:

производная суммы = сумма производных слагаемых

f'(tg^2(x)) = 2tg(x) * (1/cos(x))^2 = 2sin(x)/cos(x)^3 // расписали как производную сложной функции

f'(-3cosx) = 3sinx

итого: 2sin(x)/cos(x)^3 + 3sinx