Ответы
Ответ дал:
0
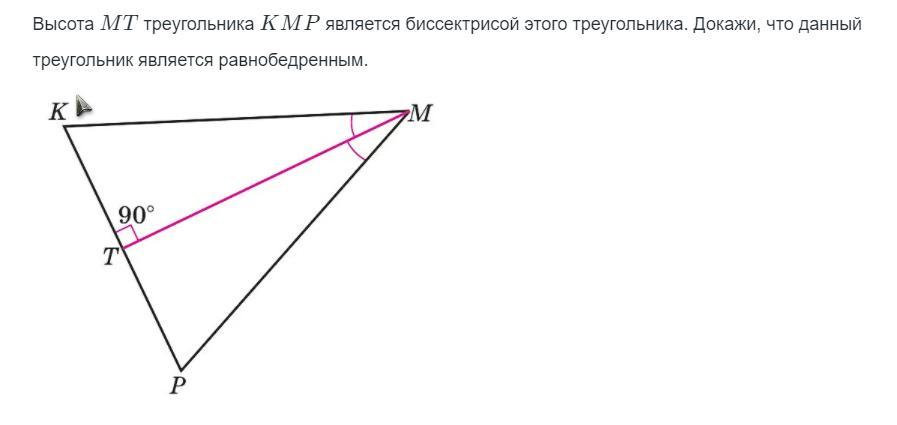
Ответ:На чертеже видно,что МТ не только биссектриса,но и высота,опущенная на основание перпендикулярно
Чтоб доказать,что треугольник КМР равнобедренный,докажем,что треугольники КМТ и МТР равны между собой
У них общая сторона МТ
Угол М биссектриса поделила на два равных угла-угол КМТ и угол ТМР
Угол КТМ равен углу МТР
Поэтому мы можем утверждать,что треугольник КМТ равен треугольнику МТР по второму признаку равенства треугольников-если сторона и два прилежащих к ней угла одного треугольника равна стороне и двум прилежащим к ней углам другого треугольника,то эти треугольники равны между собой
Следовательно
КМ=МР
И треугольник КМР является равнобедренным
Объяснение:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад