ХЕЕЕЕЕЕЕЕЕЕЛПППППППП!!!!!!
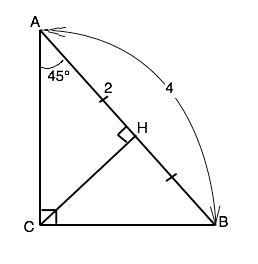
1.Найти катеты прямоугольного треугольника, если гипотенуза равна 4 см, а
одиниз углов 45 градусов.
Ответы
Ответ: 2√2 см
Сумма острых углов прямоугольного треугольника 90°, поэтому второй острый угол данного треугольника тоже 45°. Треугольник, в котором равны два угла,– равнобедренный. АС=ВС .
На сайте достаточно таких задач с разными величинами сторон, которые решены по т.Пифагора или с помощью синуса (косинуса) острого угла. Но подобные задачи нередко можно решить устно, мысленно разделив такой треугольник на два равных.
Объяснение.
Пусть в треугольнике АВС из острого угла проведена высота СН. В равнобедренном треугольнике высота является медианой и делит сторону, к которой проведена, пополам.
В равнобедренном прямоугольном треугольнике высота, проведенная из прямого угла, делит его на два равных прямоугольных треугольника равными катетами. АН=ВН=СН=2.
АС - гипотенуза ∆ АНС, ВС - гипотеуза ∆ ВНС.
Гипотенуза равнобедренного прямоугольного треугольника, как и диагональ квадрата, равна произведению стороны, содержащей прямой угол, на √2. АС=ВС=АН•√2=2√2 см.