Ответы
Ответ дал:
1
Ответ:
15 кв. ед.
Объяснение:
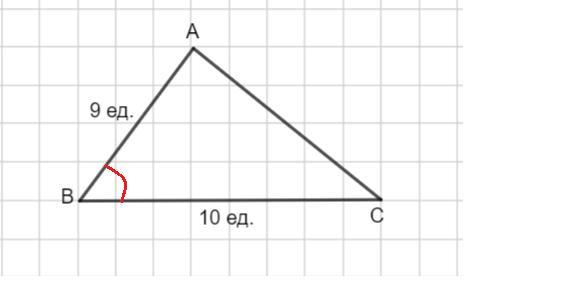
Рассмотрим треугольник ABC.
AB=9ед., BC=10ед.,
Найдем площадь треугольника по формуле:
где α - угол между сторонами a и b.
Значит, площадь треугольника равна 15 кв. ед.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад