Ответы
Ответ дал:
0
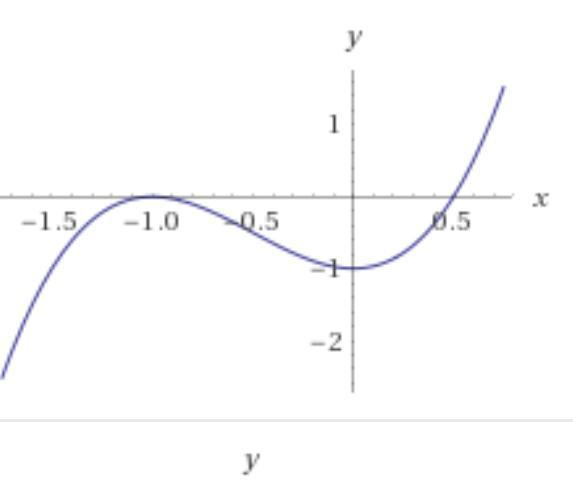
Дана функция у = 2x^3 + 3x^2 - 1.
Её производная равна у = 6x^2 + 6x = 6x(x + 1).
Приравняем её нулю: 6x(x + 1) = 0 и получаем 2 критические точки:
x = 0 и x = -1.
Находим знаки производной на промежутках между полученными точками.
x = -2 -1 -0,5 0 1
y' = 12 0 -1,5 0 12 .
Ответ: на промежутках (-∞; -1) и (0; +∞) функция возрастает.
На промежутке (-1; 0) функция убывает
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад