Question

Срочно!!!
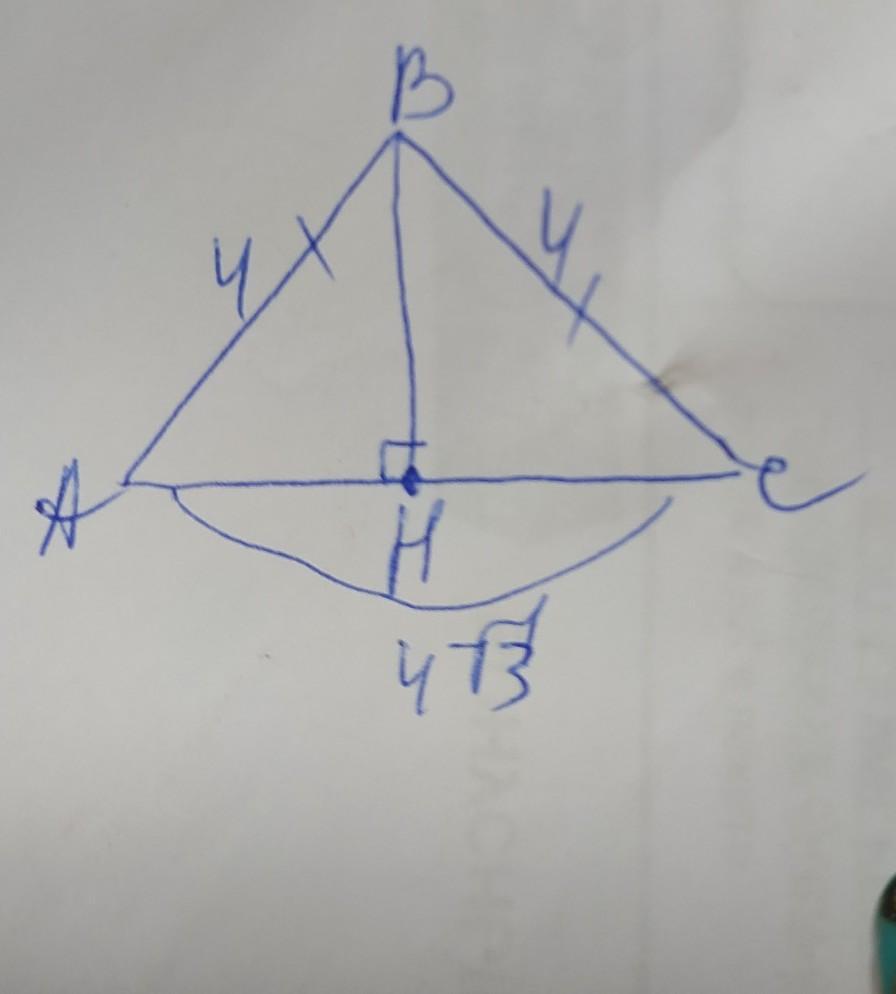
Основание равнобедренного треугольника равно 4√3 см, а боковая сторона равна 4см. Найдите высоту опущенную к основанию и углы треугольника​

Answer 1

Ответ:

ВН=2см

Объяснение:

Обозначим вершины треугольника А В С, высоту ВН. ВН делит ∆АВС на 2 равных прямоугольных треугольника, в которых высота и половины являются катетами, а боковые стороны - гипотенузы, и ещё ВН является ещё биссектрисой и медианой, так как ∆АВС равнобедренный, поэтому <АВН=<СВН, АН=НС=4√3÷2=2√3см. Рассмотрим∆АВН и найдём <А, используя косинус угла. Косинус - это отношение прилежащего к углу катета к гипотенузе, поэтому

$\cos(A) = \frac{AH}{AB} = \frac{2√3}{4} = \frac{√3}{2} =30°$

Так как <А=30°, то ВН=1/2 АВ, поскольку катет, лежащий напротив угла 30° равен половине гипотенузы, поэтому ВН=АВ÷2=4÷2=2см