Question

Площадь паралелограмма  со сторонами 5 см и 6 см равна 24 см в квадрате .Найдите диагонали паралеллограмма

Answer 1

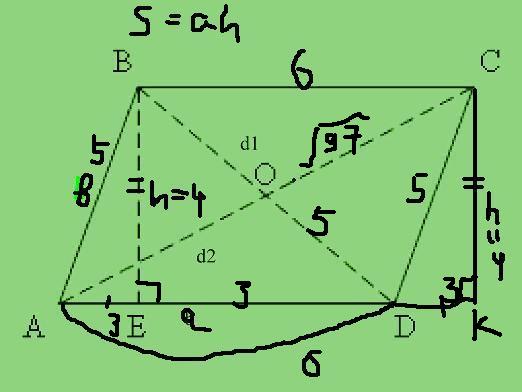
1. Рассмотрим параллелограмм АВСД.
S=ah, а= 6 это следует h=4
2.Рассмотрим Δ АВЕ, в=5, h=4. Тогда по теореме Пифагора
$x^{2} =5 ^{2} -4^{2} =9$
х=3, т.е. АЕ=ДК=3, это следует
3. ЕД=АД-АЕ=3
4. Рассмотрим ΔВЕД, по теореме Пифагора следует
$x^{2} =3^{2} + 4 ^{2} =25$
×=5,т.е. ВД=5
5.Проведем дополнительную высоту СК с вершины С и соединяем с основанием АД
6. Рассмотрим Δ АСК, АК=9, СК=4⇒ по теореме Пифагора
$x^{2} =9 ^{2} + 4 ^{2} =97$
×=√97, т.е. АС=√97

Answer 2

параллелограмм АВСД(по этому же рисунку). АВЕ: угол А и В=45град, это следует что треуг. АВЕ-равнобедренный. Тогда по теореме Пифагора следует что х2+х2=4² , следует 2х²= 16 => х²=8, х=2√2 Рассмотрим треуг. ВЕД: ЕД=6-2√2, ВЕ=2√2. Чтобы найти диагональ ВД: по теореме Пифагора следует х2=(2√2)2 + (6-2√2)2=36 => х=6

Answer 3

Спасибо,очень помогли вы мне)

Answer 4

не за что)