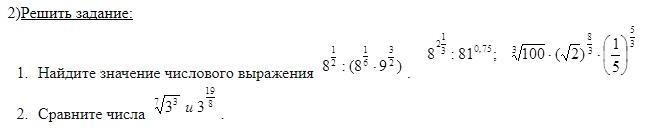Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
1.
2.
При одинаковом основании будет больше то число, у которого показатель степени больше. Сравним степени:
Следовательно,
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад