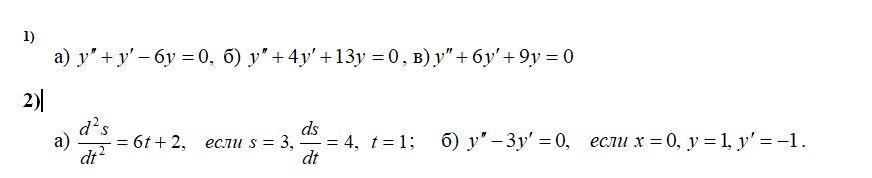Ответы
Ответ дал:
1
Ответ:
1. везде замена
a)
б)
в)
2.
а)
общее решение
система:
частное решение.
б)
замена
общее решение
система:
частное решение
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад