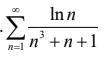Ответы
Ответ дал:
0
Ответ:
Пошаговое объяснение:
исследуем предел общего члена ряда
сначала упростим предел
тогда наш предел превращается в
- а этот рядсходится как обобщенный гармонический ряд с показателем степени p=
2
ответ исходный ряд сходится
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад