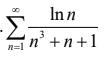Ответы
Ответ дал:
1
Ответ:
Сходится!
Объяснение:
ln n < n; n³ + n + 1 > n³, следовательно
0 < ln n/(n³ + n + 1) < 1/n³
Но ряд с общим членом 1/n³ сходится, следовательно сходится и исследуемый ряд
rumanezzo:
к сожалению не без "косяка" - там где было < 1/n³ должно быть < n/n³, ну в конце - не 1/n³, а 1/n²
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад