Помогите найти производную неявной функции. Если можно - прикрепите фото, чтобы я поняла, как именно это оформить в тетради.....
Приложения:
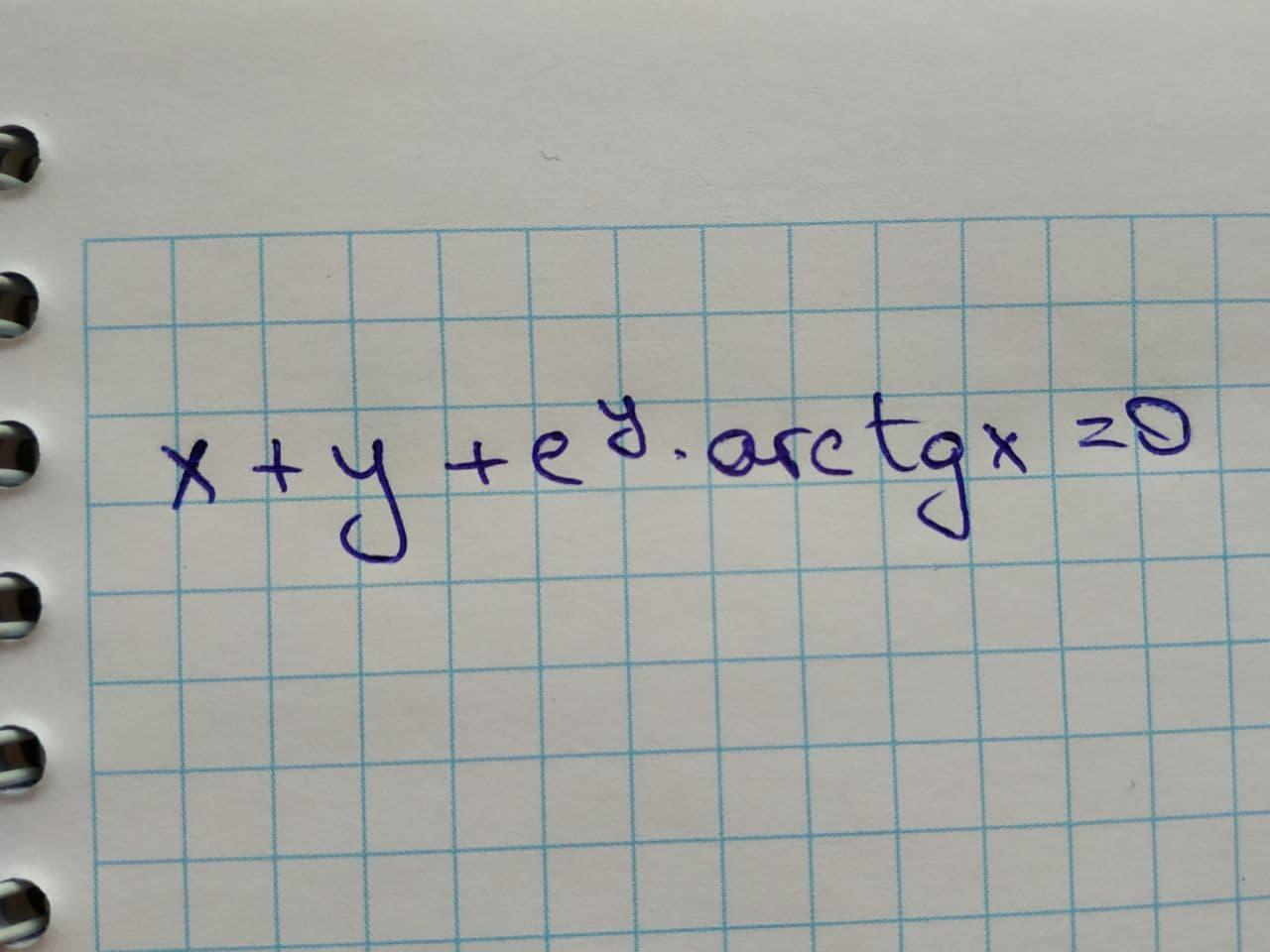
Ответы
Ответ дал:
1
Ответ:
решение на фотографии
/////
Приложения:
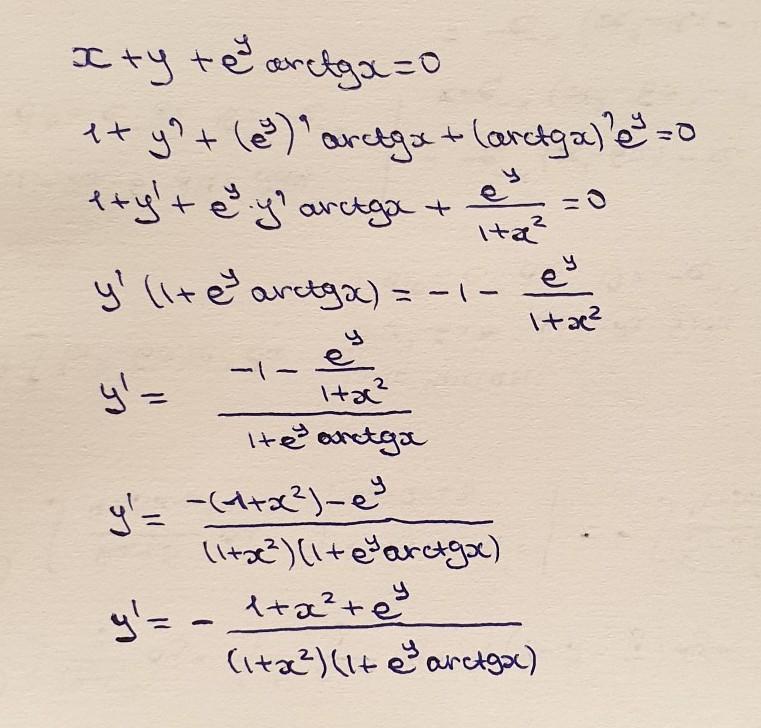
Ответ дал:
1
Ответ:
Пошаговое объяснение:
я на листочке не могу. я тут всё напишу, Вы просто можете в тетрадку переписать всё из ответа. дословно переписывайте и всё.
итае, поехали
имеем функцию
поскольку функция задана в неявном виде, то производную ищем по формуле:
находим частные производные f(x,y) по х и f(x,y) по y
таким образом производная от равна
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад