Question

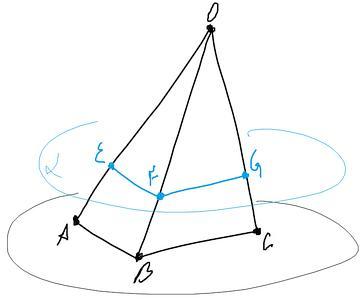
Даны четыре точки О,А,В,С, не лежащие в одной плоскости. Точка Е делит отрезок ОА в отношении 1:3, считая от точки А. Через точку Е проведена плоскость альфа, параллельная плоскости ( АВС ) и пересекающая отрезки ОВ и ОС соответственно в точках F и G. Найдите длину отрезка FG, если BC - 8 см

Answer 1

Если две параллельные плоскости (EFG||ABC) пересечены третьей (AOB), то линии пересечения параллельны, EF||AB.

Аналогично FG||BC.

BF/FO =AE/EO =1/3 (т о пропорциональных отрезках) => FO/BO =3/4

△FOG~△BOC (по соответственным углам)

FG/BC =FO/BO =3/4 => FG =8*3/4 =6 (см)