Ответы
Ответ дал:
1
Ответ:
(см. объяснение)
Пошаговое объяснение:
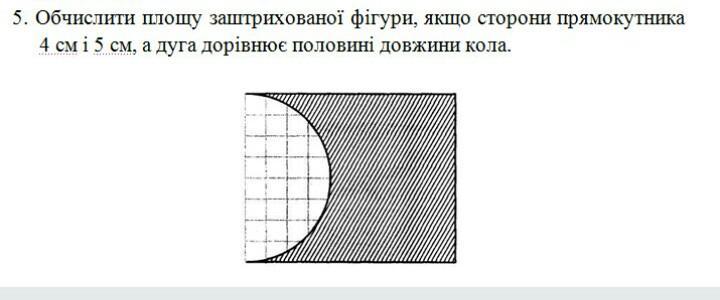
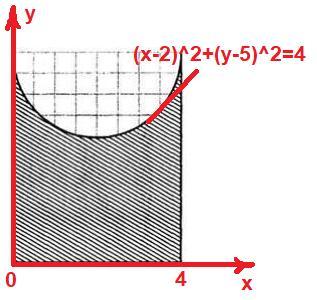
Перерисуем фигуру так, как показано на рисунке (см. фото к решению). Очевидно, что площадь заштрихованной части - это площадь под графиком окружности .
Найдем ее, вычислив определенный интеграл:
Получили, что площадь искомой фигуры равна .
Задание выполнено!
Комментарий:
Понятно, что эту задачу нужно решать путем вычитания из площади прямоугольника половины площади круга.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад