решить ............................................
Приложения:
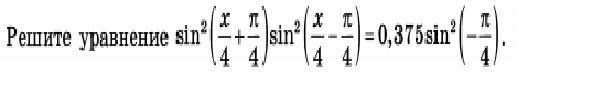
Simba2017:
из чужих приложений решений не писать....
Ответы
Ответ дал:
2
Ответ:
у вас не до конца решено?
все, поняла, большое спасибо!
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад