Очень нужно, помогите пожалуйста!!!
Используя признаки Даламбера и Коши исследовать сходимость рядов.
Приложения:
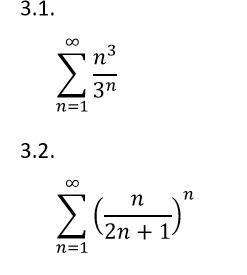
Ответы
Ответ дал:
5
Ответ:
Пошаговое объяснение:
3.1
признак Даламбера
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 -
q < 1 - ряд сходится
3.2
признак Коши
q < 1 - ряд сходится
pandacooll28:
А можно 3.2. еще, пожалуйста!
я 3,2 решила по признаку Коши. только вот ошиблась в числителе вместо n поставила 2. но ответ правильный. попробую поправить
Буду ждать
что-то не шлю мне на исправление.... вы просто во второй строчке снизу под корнем вместо числителя 2 поставьте n и дальше, после знака равенства в лимите дробь должна быть n/(2n+1)
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад