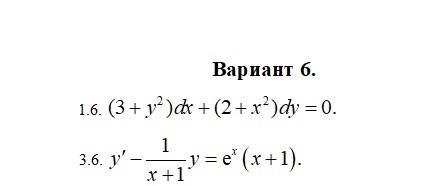Ответы
Ответ дал:
1
Ответ:
1.6
Это ДУ с разделяющимися переменными
общее решение
3.6
это линейное ДУ
замена:
общее решение
unknownsecret75:
лучший бро, спасибо
Вас заинтересует
2 года назад
2 года назад
2 года назад
9 лет назад
9 лет назад