Привести общее уравнение кривой второго порядка к каноническому виду и найти точки пересечения ее с прямой x-y^2-2y+2=0; x+y-2=0
16- Вариант
Приложения:

Ответы
Ответ дал:
1
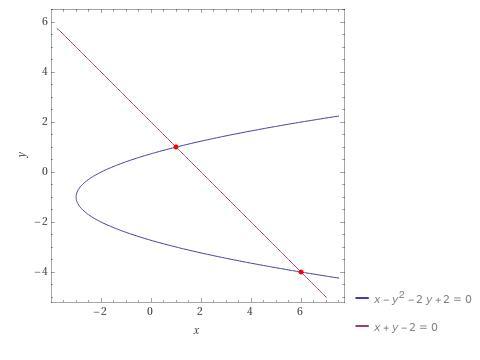
Даны уравнения кривой второго порядка x-y²-2y+2=0 и прямой x+y-2=0.
В уравнении кривой выделим полный квадрат.
x - (y² + 2y + 1) + 1 +2=0,
(y + 1)² = x + 3, приведём к каноническому виду.
(y - (-1))² = 2*(1/2)(x - (-3)).
Это уравнение параболы, ветви которой направлены вправо симметрично прямой у = -1, параллельной оси Ох, вершина в точке (-3; -1).
Точки пересечения с прямой находим решением системы.
{x-y²-2y+2=0
{x+y-2=0. x = 2 - у подставим в первое уравнение.
2 - у - y²- 2y + 2=0.
y² + 3y - 4 = 0. Д = 9 + 4*4 = 25.
х1 = (-3 + 5)/2 = 1, у1 = 2 - х = 2 - 1 = 1.
х2 = (-3 - 5)/2 = -4, у2 = 2 - х = 2 - (-4) = 6.
Ответ: точки (1; 1) и (6; -4).
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад