Найти промежутки монотонности и экстремумы функции 
Аноним:
сколько лет
Привет, я не буду отвечать на вопросы подобного характера.
пж отвечай
сколько лет,как тебе зовут?
ало
алоо отвечац
отвечай
пока
не пеши
всегда не пеши
Ответы
Ответ дал:
0
Ответ:
Объяснение:
На промежутке от (-1/2) не включая до + бесконечности функция возрастает, точка (-1/2) является точкой экстремума функции
Приложения:
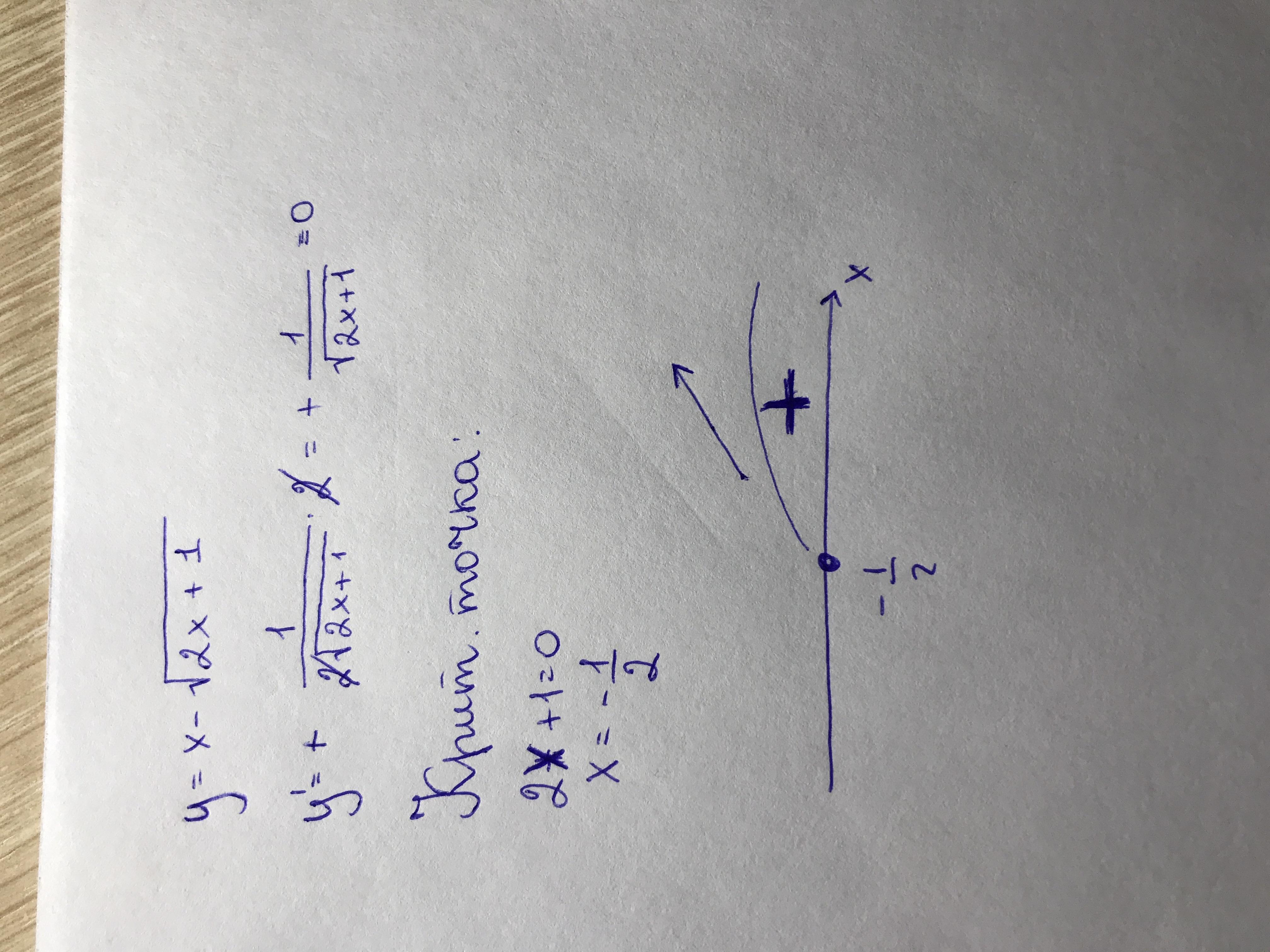
Ответ дал:
1
Ответ:
Объяснение:
1) ОДЗ: 2x+1>=0, 2x>=-1, x>= -1/2
2) y'=1 - 1/ 2 V(2x+1) *(2x+1)' = 1 - 1/V(2x +1) , (2x +1 под корнем V)
3) y'=0, 1 - 1/ V(2x+1) = 0, 1= 1/V(2x+1), (V(2x+1) =1, 2x+1=1, 2x=0,
x=0 -критич. точка [-1/2] - - - - - [0] + + + + +, производная меняет знак
с (- ) на (+), значит, 0 - точка min, функция убывает на [-1/2; 0] и
возрастает на [0; +беск-ть)
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад