Найти производные dy/dx с объяснением (шагами):
Приложения:
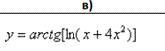
Аноним:
могу скинуть решение с подробными шагами в инсту
@1oxygenium
жду
Ответы
Ответ дал:
0
Ответ:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад