Ответы
Ответ дал:
0
Решение:
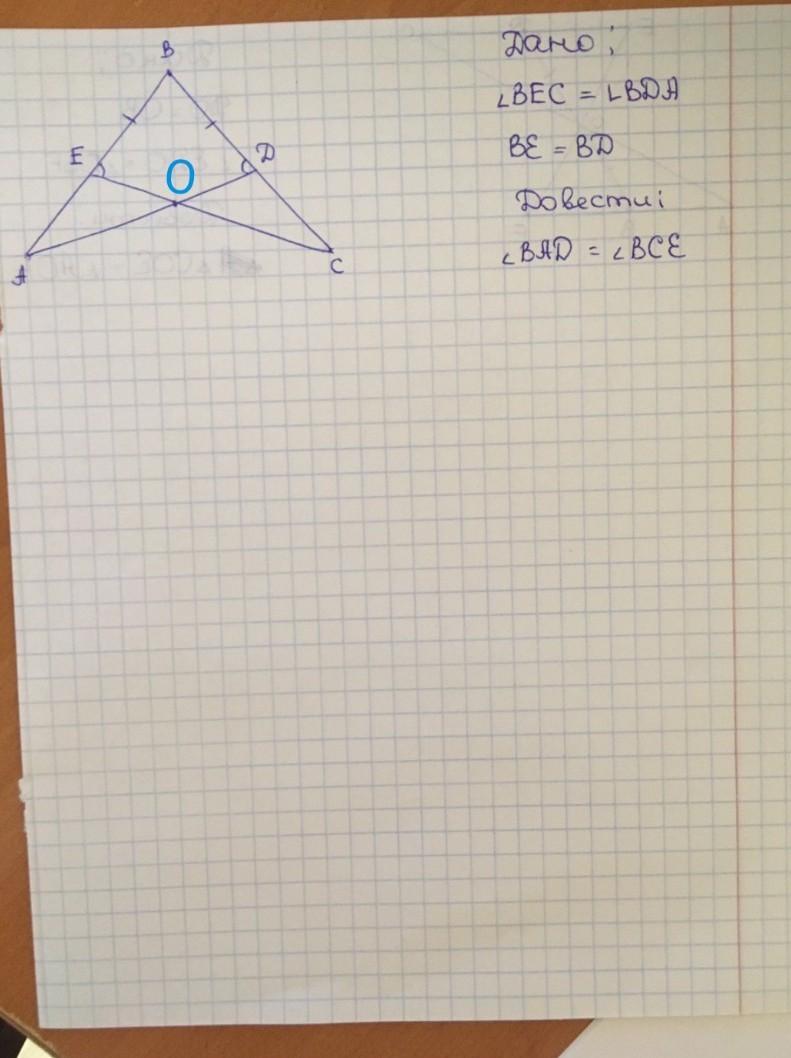
Рассмотрим треугольники АВD и ВЕС. Угол BDA= углу ВЕС, угол АВD= углу CBE (это один и тот же угол; общий), и ВЕ=ВD (из условия). Тогда треугольник АВD = треугольнику ВЕС по двум углам и стороне между ними. А это значит, что угол ВАD= углу ВСЕ (они в равных треугольниках занимают одно место).
Доказано.
salam837:
спасибочки
Ответ дал:
1
1) Рассмотрим треугольники ABD и BEC.
1. BE=BD (по условию).
2. ∠BEC=∠BDA (по условию).
3. ∠ABC - общий.
→ ΔABD = ΔBEC по стороне и двум прилежащим углам.
2) Т.к. ΔABD = ΔBEC, то их элементы соответственно равны, значит, ∠BAD=∠BCE, что и требовалось доказать.
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад