Question

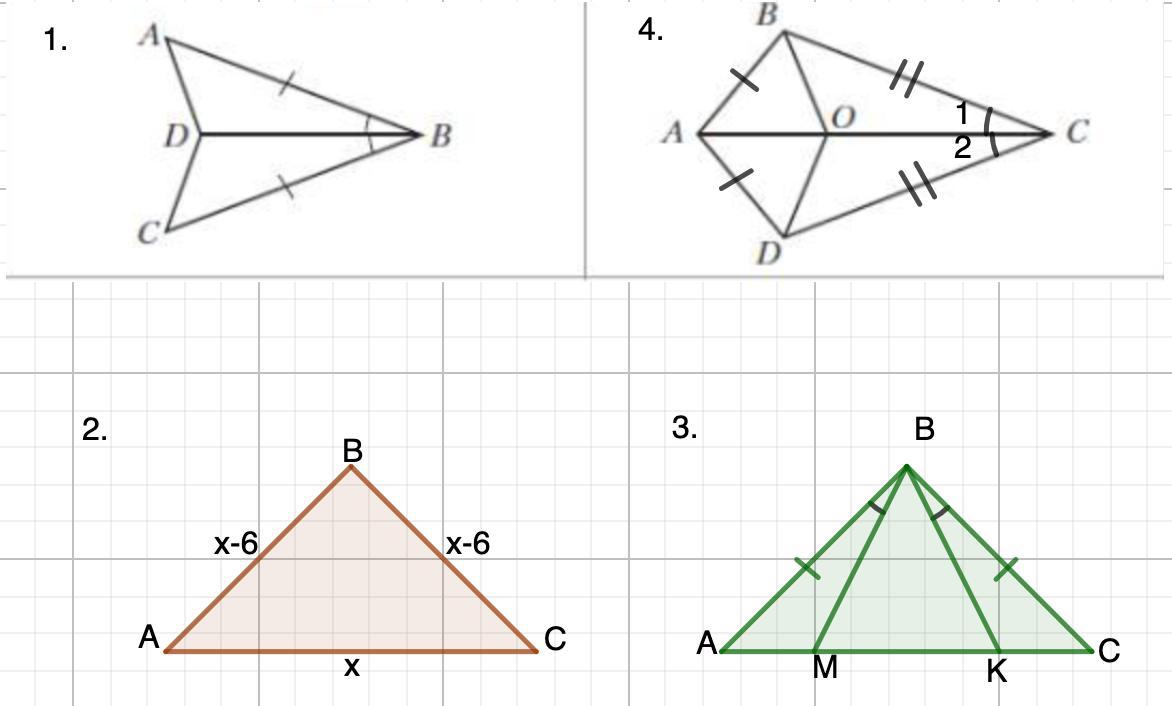
1. Докажите равенство треугольников ABD и CBD (рис. 44), если AB = BC и ∠ABD =∠CBD.

2. Найдите стороны равнобедренного треугольника, если его периметр равен 30 см, а боковая сторона на 6 см меньше основания.

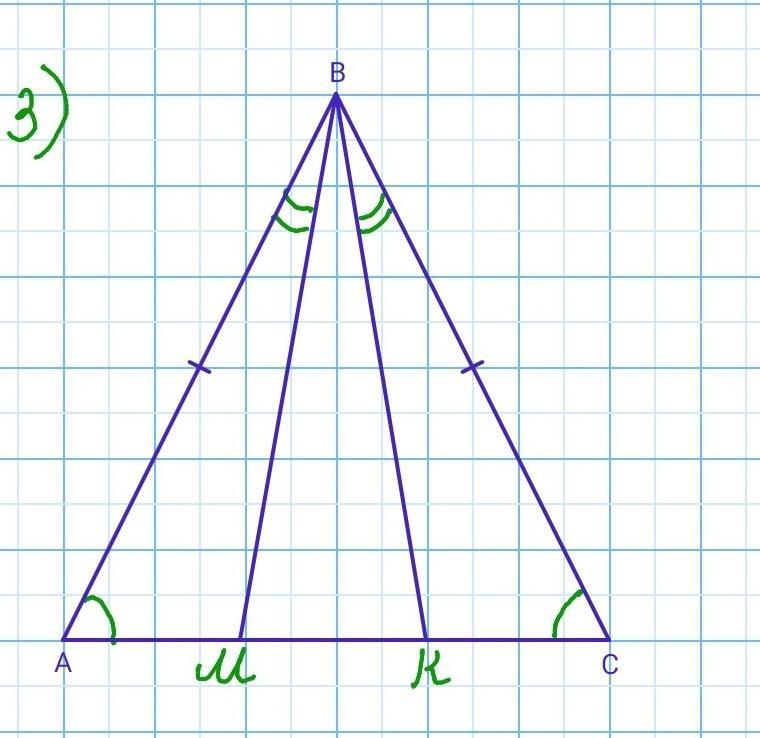
3. На основании AC равнобедренного треугольника ABC отметили точки M и K так, что ∠ABM =∠CBK, точка M лежит между точками A и K. Докажите, что AM = CK.

4. Известно, что AB = AD и BC = DC (рис. 45). Докажите, что BO = DO.

Answer 1

Объяснение:

1) AB=ВС, ∠ABD =∠CBD - по условию, BD - общая. △ABD = △CBD по двум сторонам и углу между ними. (1 признак равенства треугольников)

2) Боковые стороны равнобедренного треугольника равны. Пусть основание треугольника равно х см, тогда боковая сторона равна (х-6)см.

Периметр треугольника - это сумма всех его сторон. Периметр = 30 см (по условию)

2(х-6)+х=30

2х+х=30+12

3х=42

х=14 см

Боковые стороны равны 14-6=8 см, основание 14 см

3) Рассмотрим △АВМ и △CBК.

∠ABM =∠CBK - по условию.

Т.к. треугольник АВС - равнобедренной, то: АВ=ВС, ∠BАM =∠BСK.

△АВМ = △CBК по стороне и двум прилегающим к ней углам (2 признак равенства треугольников).

Из равенства треугольников следует, что AM = CK

4) Рассмотрим треугольники АВС и ADC.

AB = AD и BC = DC - по условию, АС - общая.

△АВС = △ADC по трём сторонам (3 признак равенства треугольников).

Из равенства треугольников следует равенство углов: ∠ВАО =∠DAO.

△АВO = △ADO по двум сторонам и углу между ними (1 признак равенства треугольников) : AB = AD - по условию, АО - общая, ∠ВАО =∠DAO - из доказанного выше.

Answer 2

Объяснение:

1. Дано: ΔABD и ΔCBD.

AB = BC и ∠ABD =∠CBD.

Доказать: ΔABD = ΔCBD.

Доказательство:

Рассмотрим ΔABD и ΔCBD.

AB = BC и ∠ABD =∠CBD (по условию)

DB - общая.

⇒ ΔABD = ΔCBD (по двум сторонам и углу между ними. 1 признак).

2. Дано: ΔАВС - равнобедренный.

АВ = (АС - 6) см.

$P_{ABC}=30\; _{CM}$

Найти: АВ; АС; ВС.

Решение:

Пусть АС = х см, тогда АВ = ВС = (х-6) см

• Периметр - сумма длин всех сторон.

Составим уравнение:

$AB+BC+AC = 30\\\\x+(x-6)+(x-6)=30\\\\3x=42\\\\x=14$

⇒ АС = 14 см; АВ = ВС = 14 см - 6 см = 8 см.

3. Дано: ΔАВС - равнобедренный.

∠ABM =∠CBK.

Доказать: АМ = СК.

Доказательство:

Рассмотрим ΔABM и ΔCBK.

АВ = ВС (ΔАВС - равнобедренный)

∠ABM =∠CBK (по условию)

• Углы при основании равнобедренного треугольника равны.

⇒ ∠А = ∠С

⇒ ΔABM = ΔCBK (по стороне и двум прилежащим углам. 2 признак).

• В равных треугольниках против равных углов лежат равные стороны.

⇒ АМ = СК.

4. Дано:

AB = AD и BC = DC.

Доказать: BO = DO.

Доказательство:

1. Рассмотрим ΔАВС и ΔACD.

AB = AD; BC = DC (по условию)

АС - общая.

⇒ ΔАВС = ΔACD (по трем сторонам. 3 признак)

• В равных треугольниках против равных сторон лежат равные углы.

⇒ ∠1 = ∠2.

2. Рассмотрим ΔОВС и ΔDOC.

ВС = DC  (по условию)

∠1 = ∠2 (п.1)

ОС - общая.

⇒ ΔОВС = ΔDOC (по двум сторонам и углу между нами. 1 признак)

• В равных треугольниках против равных углов лежат равные стороны.

⇒ ОВ = OD