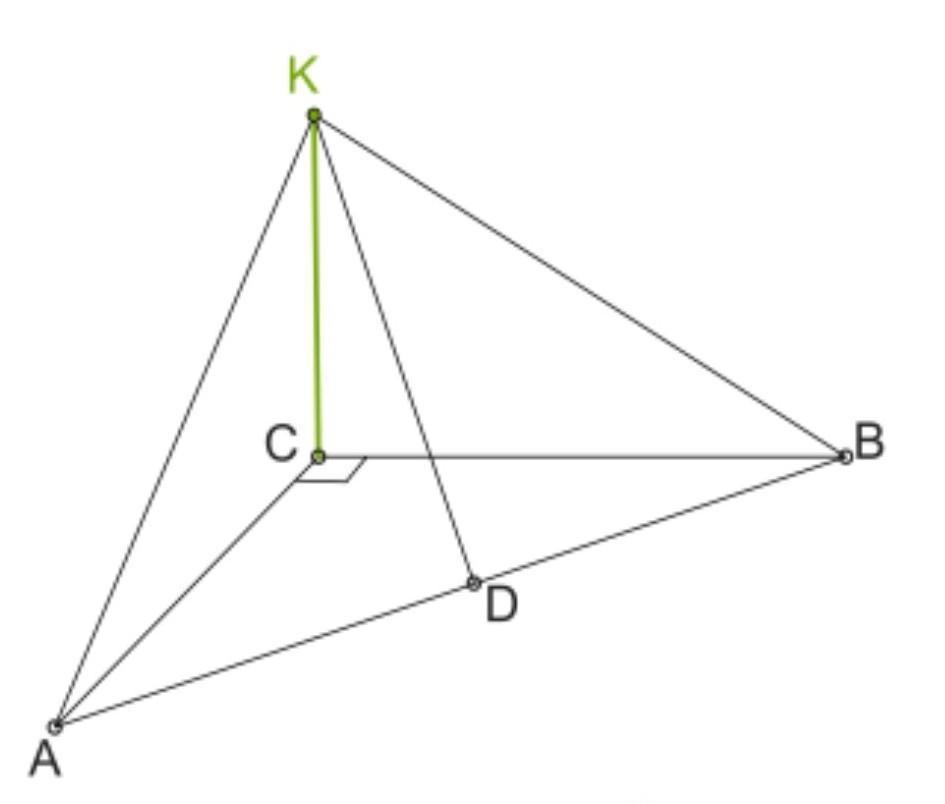
Через вершину прямого кута C до площини прямокутного
трикутника ABC проведена перпендикулярна пряма KC.
Точка D — серединна точка гіпотенузи AB.
Довжина катетів трикутника AC = 6 мм і BC = 8 мм.
Відстань KC = 12 мм. Визнач довжину відрізка KD.
Даю 25 балов
Приложения:
Ответы
Ответ дал:
12
Ответ:
КD=13мм
Объяснение:
По теореме Пифагора найдем
АВ=√(АС²+СВ²)=√(6²+8²)=√(36+64)=√100=
=10мм.
АD=AB:2=10:2=5мм
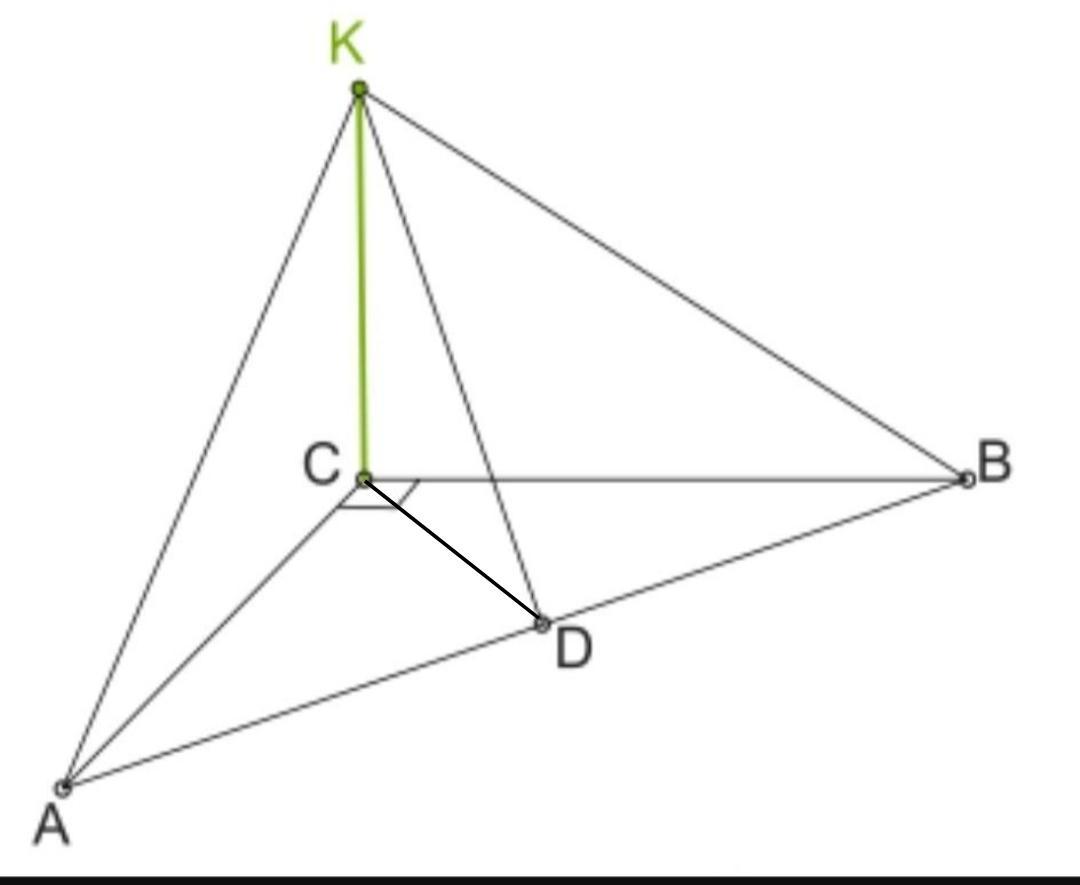
СD=AD=DB, так как CD медиана прямоугольного треугольника.
СD=5мм.
∆КСD- прямоугольный треугольник.
КD- гипотенуза.
КС и СD- катеты.
По теореме Пифагора найдем
КD=√(KC²+CD²)=√(12²+5²)=√(144+25)=
=√169=13мм
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад