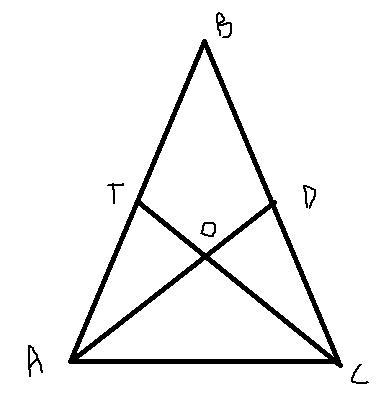
Медианы AD и CT изображены в треугольниках ABC. Известно, что AD = CT. Докажите, что AB = BC.

Помогите, пожалуйста!

Warlock1: к задаче нет конкретного рисунка, то есть просто якобы даны два медианы?

Аноним: Где рисунок?

nastyanastya419: в задании надо самому нарисовать рисунок

Warlock1: в таком случае текст задания очень кривой

nastyanastya419: ну уж не я писала задание

Warlock1: ну я напишу решение, но если я не так понял задачу, то извини, скажи, чтобы писали по-человечески

nastyanastya419: ок, главное хоть какой то был ответ, просто мне нужно до 8 сегодня сдать

Warlock1: jr

Warlock1: ок

nastyanastya419: спасибо большое!

Ответы

Ответ дал: Warlock1

Ответ:

Объяснение:

Пусть медианы AD и СТ пересекаются в точке O. По свойству медиан треугольника, в этой точке они делятся в отношении 2:1. То есть CO=2*OT, AO=2*OD. Поскольку по условию задачи AD=CT, то и OT=OD, CO=AO. Кроме того в треугольниках △AOT и △COD углы <AOT=<COD как вертикальные. Значит △AOT=△COD по 1му признаку. => <TAO=<DCO (1)

Из равенства CO=AO следует, что △AOC - равнобедр. => <OAC=<OCA (2)

Суммируя выводы (1) и (2) делаем заключение, что и углы <BAC=<BCA как суммы равных углов <TAO+<OAC=<DCO+<OCA

А значит треугольник △ABC - равнобедренный и AB=BC чтд.

Приложения: