Question

Площадь прямоугольника ABCD равна 46 см² . Найди площадь треугольника AED. дам 20баллов

Answer 1

Ответ:

23 см²

Объяснение:

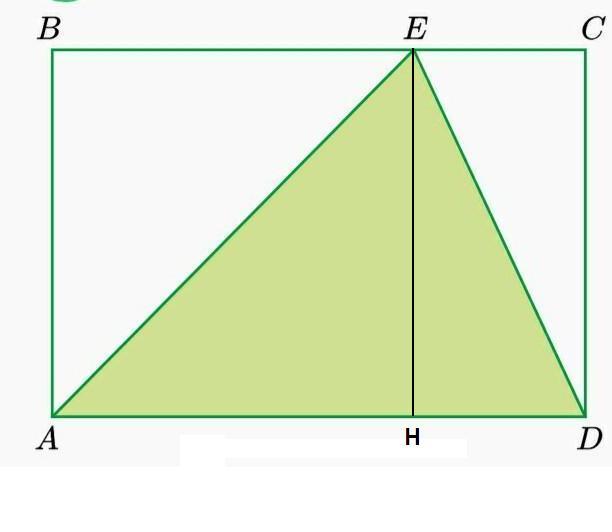
Проведем ЕН║АВ.

Отрезок ЕН разбивает прямоугольник ABCD на два прямоугольника:

ABEH и ECDH.

Диагональ АЕ делит прямоугольник АВЕН на два раных треугольника:

АВЕ и ЕНА. Значит, площадь треугольника ЕНА равна половине площади прямоугольника АВЕН:

$S_{EHA}=\dfrac{1}{2}S_{ABEH}$.

Аналогично, площадь треугольника EHD равна половине площади прямоугольника ECDH:

$S_{EHD}=\dfrac{1}{2}S_{ECDH}$

Площадь треугольника AED равна сумме площадей этих треугольников, значит , равна половине площади прямоугольника ABCD:

$S_{AED}=S_{EHA}+S_{EHD}=\dfrac{1}{2}S_{ABEH}+\dfrac{1}{2}S_{ECDH}=\dfrac{1}{2}S_{ABCD}=\dfrac{1}{2}\cdot 46=23$  см²