Question

4.
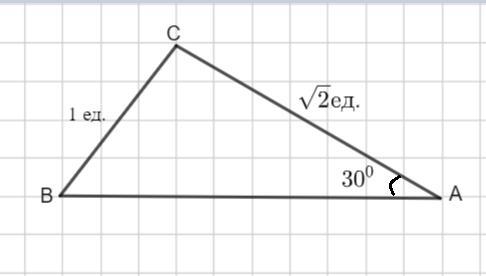
В остроугольном треугольнике ABC даны две стороны ВС =1,АС = √2 и угол А равный 30.
Найдите угол В.​

Answer 1

Ответ:

∠B =45°.

Объяснение:

Рассмотрим треугольник АВС.

Воспользуемся теоремой синусов: стороны пропорциональны синусам противолежащих углов.

$\dfrac{BC}{sinA} =\dfrac{AC}{sinB} ;\\\\sinB= \dfrac{AC\cdot sinA}{BC} ;\\\\sinB=\dfrac{\sqrt{2} \cdot sin30^{0} }{1} =\dfrac{\sqrt{2} \cdot \dfrac{1}{2} }{1} =\dfrac{\sqrt{2} }{2}$

∠B =45°