Question

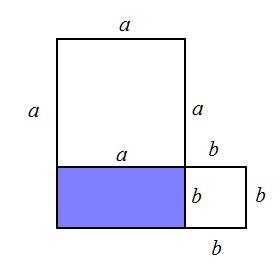
Дан прямоугольник со сторонами a и b. На его сторонах построены квадраты. Площадь одного квадрата на 21 см2 больше площади другого. Найди площадь прямоугольника, если длина прямоугольника на 3 см больше его ширины.


можно пожалуйста с решением​

Answer 1

Нужно знать:

1) площадь прямоугольника находят по формуле S = ab, где a и b его стороны;

2) площадь квадрата находят по формуле S = a², где а - сторона квадрата.

По условию для определенности а - длина, b - ширина (см. рисунок к задаче), тогда а = b + 3, b = a - 3 и площади квадратов будут равны:

S₁ = a², S₂ = b² = (а - 3)². Т.к. S₁ больше S₂ на 21 см², то составим и решим уравнение

а² - b² = 21 или а² - (а - 3)² = 21,

а² - а² + 6а - 9 = 21,

6а = 21 + 9,

6а = 30,

а = 30 : 6,

а = 5.

Значит, длина прямоугольника равна 5 см, тогда ширина

b = а - 3 = 5 - 3 = 2 (см), а площадь S = ab = 5 · 2 = 10 (см²).

Ответ: 10 см².